Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(n\left(\Omega\right)=C^4_8\cdot C^4_4\)
X: "2 bạn Việt và Nam nằm chung 1 bảng"
Số cách xếp là:
\(n\left(X\right)=C^1_2\cdot C^2_6\cdot C^4_4\)
=>P=3/7

Đáp án B
Số phần tử của không gian mẫu là: ![]()
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: ![]()
Vậy xác suất cần tính
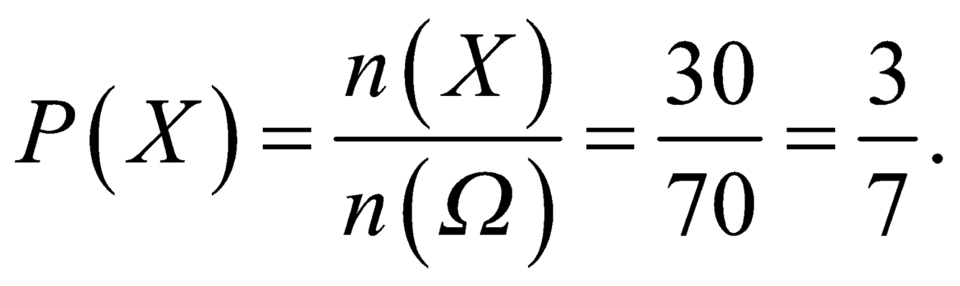

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

Chọn B
Gọi 2 cặp vợ chồng là C1-V1 và C2-V2 (C=chồng, V=vợ).
* Số cách chọn ra 7 đôi:
- Đầu tiên chọn ra 7 nam trong 10 nam: C 10 7 (cách).
- Xếp 7 người nam này thành 1 hàng ngang, người đầu tiên có 12 cách ghép với nữ, người thứ hai có 11 cách, cứ như thế suy ra số cách ghép đôi là 12.11.10.9.8.7.6 (cách).
- Theo quy tắc nhân có 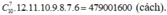
* Số cách chọn 7 đôi, chỉ có một cặp vợ chồng
- Trường hợp 1: chỉ có cặp vợ chồng C1-V1, khi đó lấy 6 nam trong 9 nam còn lại:
+ Nếu trong 6 nam này không có C2 thì số cách ghép 6 cặp còn lại là: ![]()
+ Nếu trong 6 nam này có C2 thì số cách ghép 6 cặp còn lại là: có 10 cách ghép C2 với nữ (trừ V2 và trừ V1), 5 nam còn lại có cách, số cách ghép cặp cho 5 nam này là 10.9.8.7.6 cách. Vậy theo quy tắc nhân có ![]()
Theo quy tắc cộng, có ![]()
- Trường hợp 2: chỉ có cặp vợ chồng C2-V2, tương tự như trên có 26248320(cách)
Vậy xác suất cần tính là: ![]()

Đáp án B
Gọi A là biến cố xảy ra trường hợp để yêu cầu.Không gian mẫu
![]()
Xét các trường hợp có thể xảy ra biến cố A là.
+) 2 nam Toán, 2 nữ Lý: C 8 2 . C 7 2 = 588
+) 2 nữ Toán, 2 nam Lý: C 7 2 . C 5 2 = 210
+) 1 nam Toán, 1 nam Lý, 1 nữ Toán, 1 nữ Lý
C 7 1 . C 5 1 . C 7 1 . C 8 1 = 1960
Số cách chọn cần tìm
![]()
Xác suất cần tìm là. 197 495




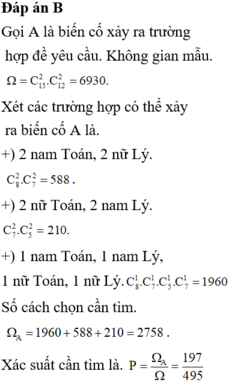
Tổng số trận đấu của các vận động viên: \(C_{3n}^2\)
Gọi số trận thắng của nữ là x thì của nam là \(_{C_{3n}^{ }^2}\)- x
Lập tỉ số và đưa về pt: 8.x = 7.n.(3n-1)
Vậy n(3n-1) phải chia hết cho 8, do đó n=3, 11, ......
Tùy theo đáp án của trắc nghiệm mà các bạn chọn đáp số.