Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
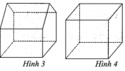
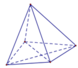
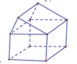
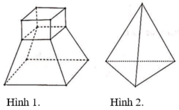
Khối đa diện (H) được gọi là khối đa diện lồi khi đoạn thẳng nối hai điểm bất kì của (H) đều thuộc (H).
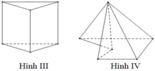
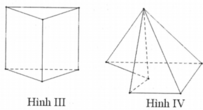
Hình (IV) có đoạn thẳng AB không thuộc khối.

Đáp án C
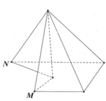
Ta có đường nối hai điểm MN không thuộc hình IV nên đây không phải là đa diện lồi

Đáp án là D.
* Nhắc lại khái niệm hình đa diện:
· Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
· Mỗi đa giác gọi là một mặt của hình đa diện. Các đỉnh, cạnh của các đa giác ấy theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.

Đáp án B
Trong hình B tồn tại 1 cạnh là cạnh chung của 3 mặt phẳng nên nó không phải là hình đa diện

Đáp án D
Nó vi phạm điều kiện thứ hai của hình đa diện, một cạnh chỉ là giao của đúng 2 mặt.

Chọn đáp án D
Áp dụng các tính chất của hình đa diện:
Mỗi cạnh là cạnh chung của đúng hai mặt.
+ Vậy đáp án D sai.

Đáp án C
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi. Một khối đa diện là đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
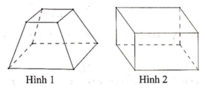
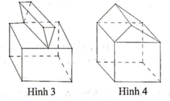
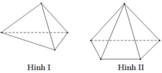

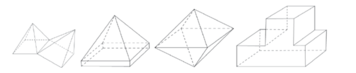

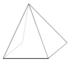

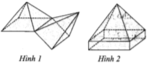
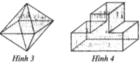
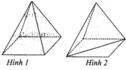


Chọn C
Áp dụng các tính chất của khối đa thức diện lồi (H)
“Đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H)’’