Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Sử dụng BĐT buhinhacopski ta có
x − 2 + y + 3 2 ≤ 1 + 1 x − 2 + y + 3 = 2 x + y + 2 .
Tức là ta có x + y + 1 2 ≤ 4 2 x + y + 2 . Đặt t = x + y . Chú ý rằng t ≥ − 1 .
Ta có
t + 1 2 ≤ 8 t + 8 ⇔ t 2 − 6 t − 7 ≤ 0 ⇔ − 1 ≤ t ≤ 7.
Vậy max t = 7 xảy ra khi x − 2 = y + 3 x + y = 7 ⇔ x = 6 y = 1 .

Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)

Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .

Đáp án C.
Ta có x x − 3 + y y − 3 + x y
= x 2 + y 2 + x y − 3 x − 3 y = x 2 + y 2 + x y + 2 − 3 x + y − 2
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ log 3 x + y − log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ ,
có f ' t = 1 + 1 t ln 3 > ; ∀ t > 0.
Suy ra f( t) là hàm số đồng biến trên 0 ; + ∞
mà f 3 x + y = f x 2 + y 2 + x y + 2
⇔ 2 x + y 2 − 6 2 x + y + 5 = − 3 y − 1 2 ≤ 0 ⇔ 1 ≤ 2 x + y ≤ 5.
Khi đó P = 1 + 2 x + y − 5 x + y + 6 ≤ 1
vì 2 x + y − 5 ≤ 0 x + y + 6 > 0 . Vậy P m a x = 1.
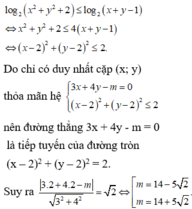
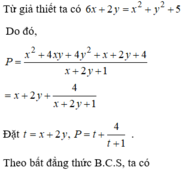
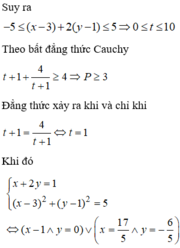
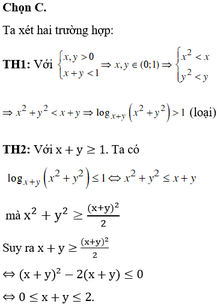
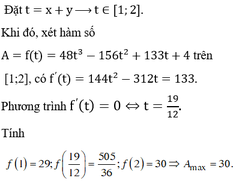



Chọn đáp án C.