Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Áp dụng lí thuyết về tính giá trị trung bình và sai số trong thưc hành thí nghi ệm
Cách giải:
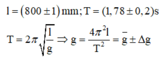
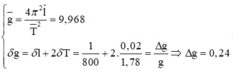
![]()

Đáp án C
Phương pháp: Áp dụng phương pháp tính sai số và công thức chu kỳ của con lắc đơn.
Cách giải:
+ Áp dụng công thức:
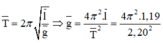
![]()
+ Sai số tương đối (ɛ):
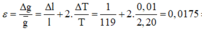
![]()
+ Gia tốc:
![]()

Đáp án B
Phương pháp :Áp dụng công thức tính sai số trong chu kỳ của con lắc đơn
Cách giải:
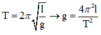
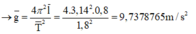
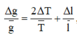
thay số ta có Dg = 0,228569601

\(S=l.\alpha_0\Rightarrow\alpha_0=\dfrac{4}{100}=0,04\left(rad\right)\)
\(\omega=\sqrt{\dfrac{g}{l}}=\pi\left(rad/s\right)\)
\(\Rightarrow\alpha=0,04\cos\left(\pi t-\dfrac{\pi}{2}\right)\left(rad\right)\)
\(S=4\cos\left(\pi t-\dfrac{\pi}{2}\right)\left(cm\right)\)

Chu kì của con lắc là: \(T=\dfrac{T'}{n}=\dfrac{14,2}{10}=1,42s\)
Ta có: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{1,42}\) rad/s
Lại có: \(\omega^2=\dfrac{g}{\Delta l}\Leftrightarrow\left(\dfrac{2\pi}{1,42}\right)^2=\dfrac{g}{50.10^{-2}}\Rightarrow g\approx9,79\)m/s2
Đáp án D

+ Con lắc thực hiện 20 dao động trong 36 s → T = 36 20
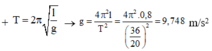
Chú ý: lấy số π theo máy tính.
ü Đáp án A
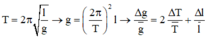
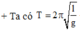
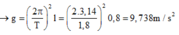
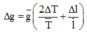
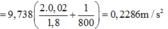
Đáp án B