Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số lần bắn trượt là x
=>Số lần bắntrúng là 20-x
Theo đề, ta có: 10(20-x)-5x=155
=>200-10x-5x=155
=>15x=45
=>x=3

Gọi số câu học sinh trả lời đúng, sai lần lược là x, y
Vì có 10 câu nên: x + y = 10 <=> x = 10 - y (1)
Học sinh được thưởng khi số điểm từ 30 trở lên nên ta có
\(5x-2y\ge30\)
Thế (1) vào ta được
\(5\left(10-y\right)-2y\ge30\)
\(\Leftrightarrow7y\le20\)
\(\Leftrightarrow y\le2\)
\(\Leftrightarrow\orbr{\begin{cases}y=1\\y=2\end{cases}\Rightarrow\orbr{\begin{cases}x=9\\x=8\end{cases}}}\)
Vậy học sinh phải trả lời đúng ít nhất 8 câu thì mới được thưởng

Gọi số câu đúng là x; số câu sai là y.
Ta có tổng số câu là 10.
Ta có hệ phương trình:
x + y = 10
10x - 5y = 85
Giải hệ ra được: x = 9 và y = 1
Vậy bạn đó trả lời đúng 8 câu.
Giả sử thì sinh đó trả lời đúng hết thì sẽ có số điểm là: \(10.10=100\)(điểm)
Vì bạn đó được 85 điểm nên số điểm bị thừa là: \(100-85=15\)(điểm)
Số câu trả lời đúng là: \(10 - 15:(5+10)= 9\)(câu)
Vậy bạn đó đã trả lời đúng \(9\) câu

1 học sinh được thưởng phải trả lời đúng ít nhất 8 câu

Gọi x là số câu trả lời đúng (0 ≤ x ≤ 10, x ∈ N)
Số câu trả lời sai: 10 – x
Trả lời đúng x câu được 5x (điểm), trả lời sai 10 –x (câu) bị trừ (10- x) điểm.
Do đó, sau khi trả lời 10 câu thì người dự thi sẽ có: 5x – (10 – x) + 10
Để được dự thi tiếp vòng sau thì
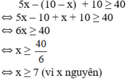
Vậy người dự thi phải trả lời chính xác ít nhất 7 câu hỏi thì mới được dự thi ở vòng sau.

Gọi số lần bắn trúng là a thì số lần bắn trật là 10 - a (a \(\in\) N, a \(\le\) 10).
Ta có tổng số điểm của xạ thủ sau khi bắn xong sẽ là: 5a - (10 - a) = 6a - 10
Để người đó được thưởng thì 30 \(\le\) 6a - 10
\(\Leftrightarrow6a\ge40\)
\(\Leftrightarrow a\ge7\)
Do đó xạ thủ phải bắn trúng đích ít nhất 7 lần.
Gọi số lần bắn trúng là a thì số lần bắn trật là 10 - a (a ∈∈ N, a ≤≤ 10).
Ta có tổng số điểm của xạ thủ sau khi bắn xong sẽ là: 5a - (10 - a) = 6a - 10
Để người đó được thưởng thì 30 ≤≤ 6a - 10
⇔6a≥40⇔6a≥40
⇔a≥7⇔a≥7
Do đó xạ thủ phải bắn trúng đích ít nhất 7 lần.