Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Giả sử ban đầu kéo m1 đến A rồi thả nhẹ, đến O nó đạt tốc độ cực đại sau đó nó va chạm đàn hồi với m2. Vì va chạm tuyệt đối đàn hồi và hai vật giống hệt nhau nên sau va chạm m1 đứng yên tại O và truyền toàn bộ vận tốc cho m2 làm cho m2 chuyển động chậm dần làm cho lò xo nén dần. Đến B m2 dừng lại tức thời, sau đó, m2 chuyển động về phía O, khi đến O nó đạt tốc độ cực đại, gặp m1 đang đứng yên tại đó và truyền toàn bộ vận tốc cho m1 làm cho m1 chuyển động đến A. Cứ như vậy, hệ dao động gồm hai nửa quá trình của hai con lắc. Do đó, chu kì dao động của hệ:


Đáp án D
+ Tại thời điểm ban đầu ta có ∆ l 0 = 10 c m
+ Đưa vật tới vị trí lò xo giãn 20 cm thì có thêm vật m2 = 0,25m1 gắn vào m1 nên khi đó ta sẽ vó VTCB mới O’ dịch xuống dưới so với O 1 đoạn bằng:
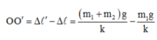

+ Khi về đến O thì m2 tuột khỏi m1 khi đó hệ chỉ còn lại m1 dao động với VTCB O, gọi biên độ khi đó là A1.
+ Vận tốc tại điểm O tính theo biên độ A’ bằng vận tốc cực đại của vật khi có biên độ là A1
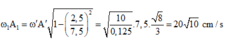
+ Biên độ dao động của m1 sau khi m2 tuột là: A 1 = 20 10 10 0 . 1 = 2 10 ≈ 6 , 32 c m

Đáp án C.
Lời giải chi tiết:
Theo giả thiết
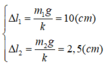
=> Tại vị trí cân bằng của hai vật lò xo dãn 12,5 cm
Thả vật tại vị trí lò xo dãn 20cm =>A=7,5cm
Khi về tới O thì lò xo dãn 10cm =>x = -2,5cm
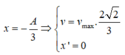
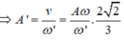
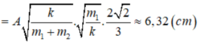

Giải thích: Đáp án A
Phương pháp: Sử dụng lí thuyết về bài toán thay đổi VTCB trong dao động điều hòa của CLLX thẳng đứng
Cách giải:
+ Tần số góc của CLLX ban đầu là: 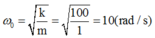
+ VTCB ban đầu của vật là vị trí lò xo giãn đoạn: 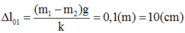
+ Tốc độ dao động của hệ hai vật khi qua VTCB là: ![]()
+ Vật m2 bị tách ra, chỉ còn vật m1 tiếp tục dao động với tần số góc: 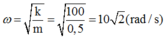
+ VTCB lúc sau của CLLX là vị trí lò xo giãn đoạn 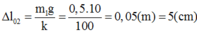
=> Khi vật m2 bị tách ra khỏi m1 thì vật đang ở vị trí có li độ x = 5 cm (so với VTCB mới), có tốc độ v= 50 cm/s, tần số góc ![]() Biên độ dao động của CLLX là:
Biên độ dao động của CLLX là:
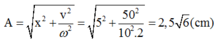

Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C

Chọn A
+ Sau khi đặt m2 lên m1 hệ dao động với tần số góc 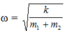
+ Để m2 không trượt trên m1 thì gia tốc chuyển động của m2 có độ lớn lớn hơn hoặc bằng độ lớn gia tốc của hệ (m1 + m2): a = -ω2x. Lực ma sát giữa m2 và m1 gây ra gia tốc của m2 có độ lớn a2 = μg = 2m/s2.
+ Điều kiện để m2 không bị trượt trong quá trình dao động là:
![]() => μg (m1 + m2) ≥ kA => m2 ≥ 0,5kg.
=> μg (m1 + m2) ≥ kA => m2 ≥ 0,5kg.
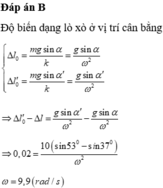

1/Khi gắn cả m1 và m2 vào lò xo ta có :
\(f=\frac{1}{2\pi}\sqrt{\frac{k}{m_1+m_2}}=2\) (*)
Nếu bớt m2 thì \(f_1=\frac{1}{2\pi}\sqrt{\frac{k}{m_1}}=2,5\) (**)
Từ (*) chia (**) ta được \(\frac{f_1}{f_2}=\sqrt{\frac{m_1}{m_1+m_2}}\Leftrightarrow\frac{2}{2,5}=\sqrt{\frac{m_1}{m_1+m_2}}\rightarrow m_1=\frac{0,64}{0,63}m_2=400g\)
Thay m1 vào (**) ta tính được k = 4pi2 . 2,52 . 0,4 = 100N/m
2/Trên mp nghiêng thì sử dụng: độ giãn delta(L) = (m.g.sin anpha)/g.
như vậy sẽ có: 0,02 (m) = (m.g).(sin53 - sin 37)/k, trong đó k/m = (omega)2
tính được: omega = 10 (rad/s)
ơ câu 1 sai rồi ạ
Chỗ f1=4 chứ ạ dẫn tới kết quả bằng 400g sai luôn
Đáp án m1=100g