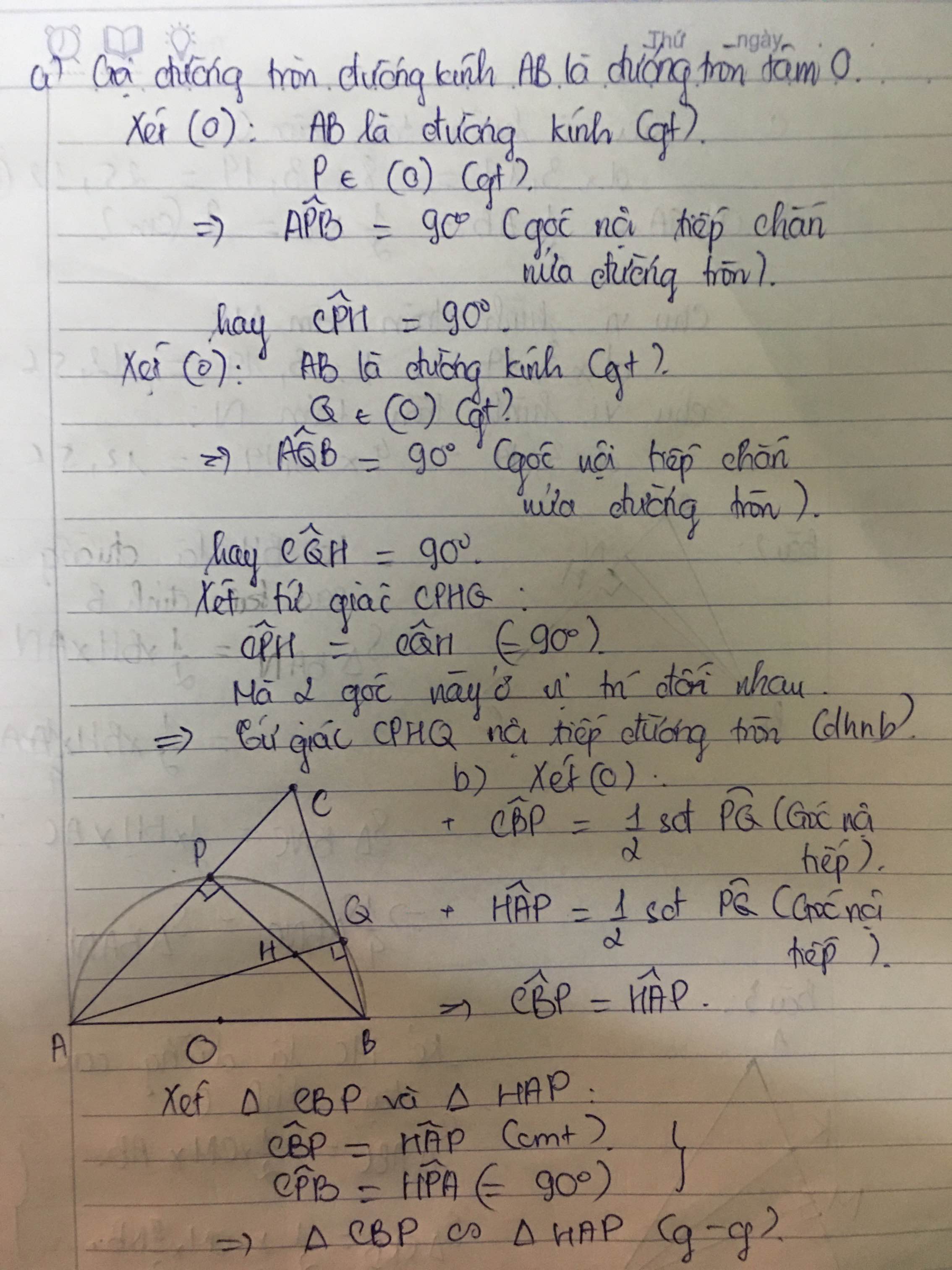Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc APB=góc AQB=1/2*180=90 độ
=>AQ vuông góc BC, BP vuông góc CA
góc CPH+góc CQH=180 độ
=>CPHQ nội tiếp

1.
Chứng minh được .
Suy ra điểm cùng thuộc đường tròn đường kính nên tứ giác nội tiếp.
Có tứ giác nội tiếp nên ( góc nội tiếp cùng chắn cung ) hay .
Trong đường tròn tâm , ta có là góc nội tiếp chắn cung và nội tiếp chắn cung
.
2.
có nên hay .
Ta chứng minh được vừa là đường cao, vừa là phân giác của tam giác nên là trung điểm của .
Chứng minh tương tự là trung điểm của là đường trung bình của tam giác (1).
Do nên là điểm chính giữa cung (2).
Từ (1) và (2) suy ra .
3.
Kẻ đường kính của đường tròn tâm , chứng minh tứ giác nội tiếp đường tròn đường kính .
Chứng minh tứ giác là hình bình hành, suy ra .
Trong đường tròn có (2 góc nội tiếp cùng chắn cung ). Chỉ ra tam giác vuông tại và áp dụng hệ thức giữa cạnh và góc ta được cm.
Đường tròn ngoại tiếp tứ giác cũng là đường tròn ngoại tiếp tam giác .
Gọi là bán kính đường tròn ngoại tiếp tam giác .
Suy ra cm.
Vậy cm.