Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
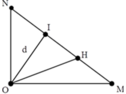
+ Gọi I là một điểm bất kì nằm trên MN
Độ lệch pha dao động giữa nguồn và I là: ∆ φ = 2 π d λ = ( 2 k + 1 ) π ⇒ d = ( 2 k + 1 ) λ 2
+ Gọi H là trung điểm của MN, khi đó dựa vào tính chất của tam giác vuông ta có O H = M N 2 = 2 13 λ
+ Số điểm dao động ngược pha với O trên đoạn NH:
2 13 λ ≤ ( 2 k + 1 ) λ 2 ≤ 12 λ ⇒ 6 , 7 ≤ k ≤ 12 , 5 → Có 5 điểm.
+ Số điểm dao động ngược pha với O trên đoạn MH: 2 13 λ ≤ ( 2 k + 1 ) λ 2 ≤ 8 λ ⇒ 6 , 7 ≤ k ≤ 7 , 5 → Có 1 điểm.
Vậy có tất cả 6 điểm dao động ngược pha với O trên đoạn MN.

Chọn A

trên đoạn AB có 5 “bó sóng” vớ O là bụng của bó trung tâm. Các bó đối xứng nhau qua một bụng thì cùng pha nên có hai điểm khác cùng pha với O

Đáp án B
Phương trình dao động của hai nguồn ![]()
Phương trình dao động của điểm M thuộc CO, cách nguồn khoảng d là:
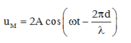
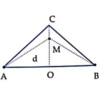
Vì điểm M dao động ngược pha với nguồn nên:
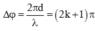
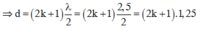
Mà ![]()
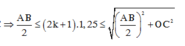
![]()
![]()
Vậy trên đoạn CO có 1 điểm dao động ngược pha với nguồn.

Đáp án A
Số điểm dao động với biên độ cực đại trên AB
- AB λ ≤ k ≤ AB λ ⇔ - 8 ≤ k ≤ 8
Để diện tích AMNB là lớn nhất thì M phải nằm trên cực đại ứng với k = –2
d1 – d2 = –2kλ = –2 cm.
Mặc khác d 1 2 = AH 2 + MH 2 d 2 2 = BH 2 + MH 2 ⇒ d 1 + d 2 = BH 2 - AH 2 2 = 16 cm .
Ta tính được d1 = 7 cm, từ đó suy ra MH = 2 5 cm .
Diện tích hình thang S AMNB = 1 2 ( AB + MN ) . MH = 18 5 cm 2 .


Đáp án: A
HD Giải: λ = 300 50 = 6cm
Số điểm dao động với biên độ cực đại, ta có:
-AB < kλ < AB
<=> -20 < 6k < 20
<=> - 3,3 < k < 3,3
Suy ra trên AB có 7 cực đại

Chọn đáp án B
I năm trên trung trực của AB =>> IOA vuông tai O.mà I cùng pha với A,B =>> IA=IB=kλ =8k I gần o nhất.mà OA=10 =>> k=2 tm =>> IA=16 =>> IO^2=IA^2-OA^2=16^2-10^2=156 => IO=căn 156 =>> B đúng

Đáp án B
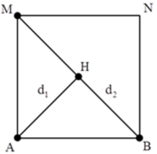
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì:
d 1 - d 2 = ( k + 1 2 ) λ
+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số d1 – d2:
AM - 2 AM ≤ d 1 - d 2 ≤ AB
+ Kết hợp hai phương trình trên ta thu được:
AM ( 1 - 2 ) λ - 1 2 ≤ k ≤ A B λ - 1 2
→ - 6 , 02 ≤ k ≤ 12 , 8
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.

Đáp án D
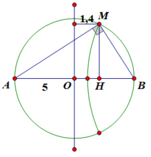
M là cực tiểu gần trung trực AB nhất nên suy ra MA – MB = 0,5λ
Có OH = 1,4 cm. Áp dụng hệ thức lượng trong tam giác vuông, có:
M A 2 = A H . A B M B 2 = B H . A B ⇒ M A = 8 ( c m ) M B = 6 ( c m ) ⇒ λ = 4 ( c m ) ⇒ v = λ . f = 60 ( c m / s )
Hướng dẫn: Chọn đáp án C
Cách 1:
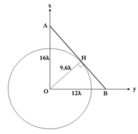
Các điểm dao động cùng pha với O cách O một số nguyên lần l. Ta vẽ các vòng tròn tâm O bán kính một số nguyên lần l. Để các vòng tròn này cắt AB thì bán kính bắt đầu từ 10l, 11l, 12l, 13l, 14l, 15l, 16l. Các đường tròn bán kính 10l, 11l, 12lcắt đoạn AB tại 2 điểm còn các đường tròn bán kính 13l, 14l, 15lvà 16lchỉ cắt đoạn AB tại 1 điểm. Nên tổng số điểm dao động cùng pha với O trên AB là 3.2 + 4 = 10 điểm ÞChọn C.
Cách 2:
Các điểm dao động cùng pha với O cách O một khoảng d = kl.
+ Số điểm trên AH: 9,6l£kl£16lÞ9,6 £k £16 Þk = 10,…16: có 7 điểm.
+ Số điểm trên HB: 9,6l< kl£12lÞ9,6 < k £12 Þk = 10,…,12: có 3 điểm.
Tổng số điểm là 10.