Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình chữ nhật ABDC có AB=5cm;AC=3cm nên diện tích ABDCABDC bằng 5.3=15( cm 2 )
Đáp án cần chọn là: A

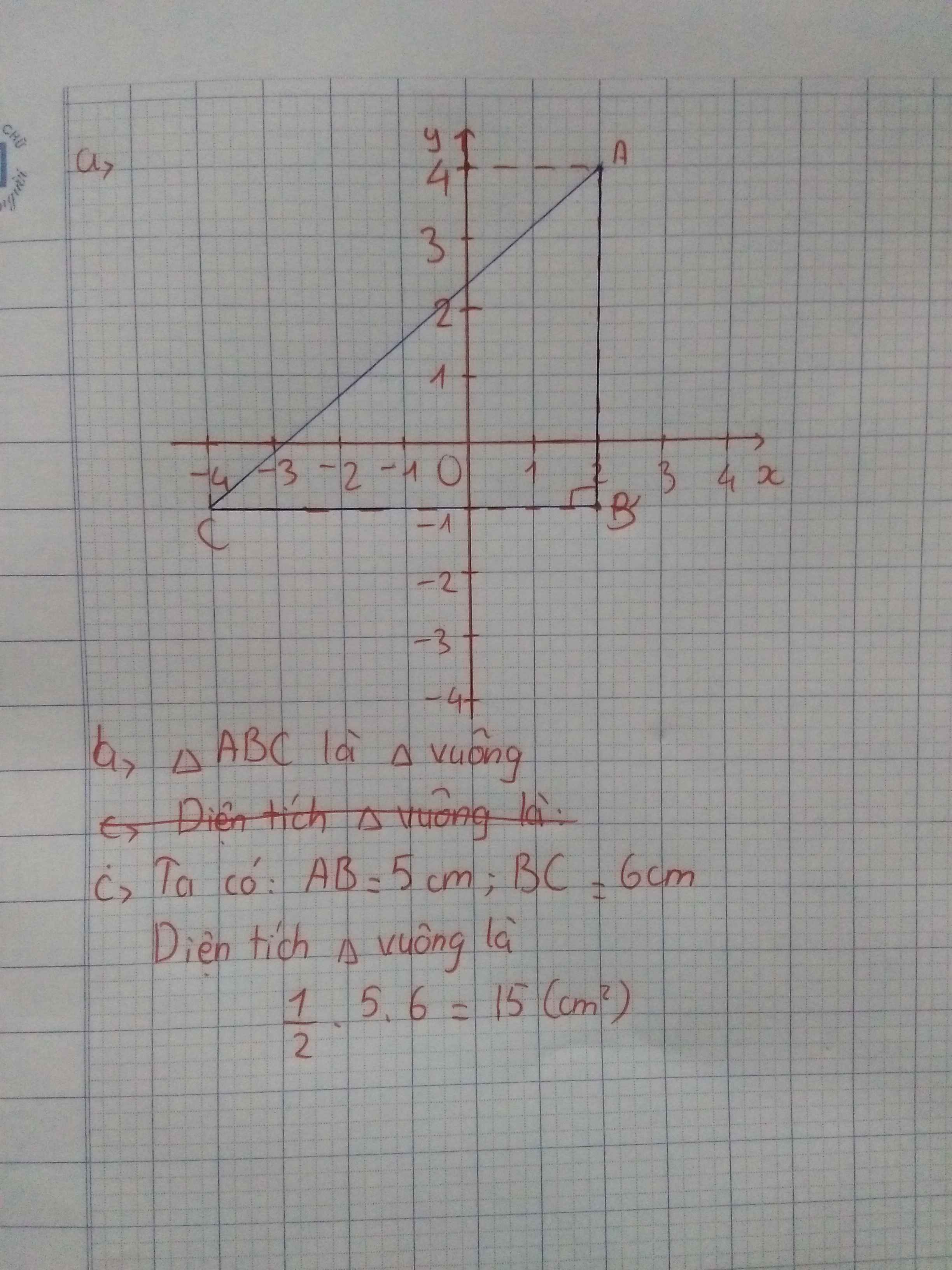
a) hình tự vẽ
b)theo hình vẽ tam giác ABC là tam giác vuông ở B
ta có AB=5,BC=6=>\(SABC=\frac{AB.BC}{2}=\frac{30}{2}=15\)(đơn vị diện tích)

Ta có :
AB = \(\sqrt{\left(1+3\right)^2+\left(4+4\right)^2}=4\sqrt{5}\)
AC = \(\sqrt{\left(1-1\right)^2+\left(4-0\right)^2}=4\)
BC = \(\sqrt{\left(-3-1\right)^2+\left(-4-0\right)^2}=4\sqrt{2}\)
=> p = \(\frac{4\sqrt{5}+4+4\sqrt{2}}{2}\)
=> \(S_{\Delta ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}=\sqrt{64}=8\)
( TÍNH THEO CÔNG THỨC HERON )
Ta có :
AB = √(1+3)2+(4+4)2=4√5
AC = √(1−1)2+(4−0)2=4
BC = √(−3−1)2+(−4−0)2=4√2
=> p = 4√5+4+4√22
=> SΔABC=√p(p−AB)(p−AC)(p−BC)=√64=8

b) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(2-2\right)^2+\left(4+1\right)^2}=5\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(2+4\right)^2+\left(4+1\right)^2}=\sqrt{61}\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(2+4\right)^2+\left(-1+1\right)^2}=6\)
Ta có: \(BA^2+BC^2=5^2+6^2=25+36=61\)
\(AC^2=\left(\sqrt{61}\right)^2=61\)
Do đó: \(AC^2=BA^2+BC^2\)(=61)
Xét ΔABC có \(AC^2=BA^2+BC^2\)(cmt)
nên ΔABC vuông tại B(Định lí Pytago đảo)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{BA\cdot BC}{2}=\dfrac{5\cdot6}{2}=\dfrac{30}{2}=15\left(cm^2\right)\)

Vẽ các điểm A(3;1);B(-2;1);C(3;4) và D(-2;4) trên cùng mặt phẳng tọa độ
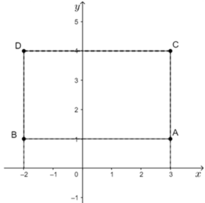
Theo hình vẽ ta thấy ABCD là hình chữ nhật
Đáp án cần chọn là B

Tam giác ABC là tam giác vuông
AB=5, BC=6
diện tích tam giác ABC là 5.6:2=15 (dvdt)