Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)

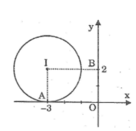
Kẻ IA ⊥ Ox
Ta có: IA = 2 = R
Suy ra đường tròn (I) tiếp xúc với trục hoành
Kẻ IB ⊥ Oy
Ta có : IB = 3 > R
Suy ra đường tròn và trục tung không có điểm chung


Kẻ \(IA\perp Ox\). Do \(IA=2=R\) nên đường tròn (I) tiếp xúc với trục hoành.
Kẻ \(IB\perp Oy\). Do \(IB=3>R\) nên đường tròn (I) và trục tung không giao nhau

Chọn đáp án C
Ta có: 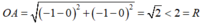
Nên A nằm trong đường tròn tâm O bán kính R = 2

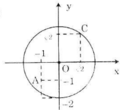
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
OC2 = (√2)2 + (√2)2 = 4 => OC = 2 = R
=> C nằm trên (O)

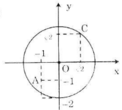
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
O C 2 = ( √ 2 ) 2 + ( √ 2 ) 2 = 4 = > O C = 2 = R
=> C nằm trên (O)