Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Để M và trung điểm I cùng pha nhau thì
![]()
→ M gần I nhất → k=1 và ![]()
Để N gần M nhất, N phải nằm trên dãy cực tiểu giao thoa ứng với k = 0
Ta có:


![]()
Kết hợp với chức năng Shift → Solve của Casio, ta tìm được
![]()
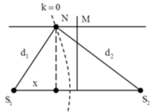

Chọn D bạn nhé, vì hai nguồn ngược pha nên hai sóng tới ngược pha.

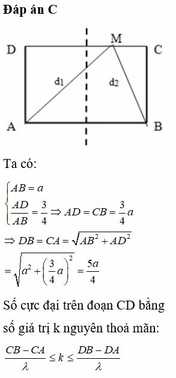
Đáp án C
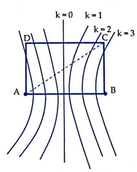
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3
⇒ 2 λ ≤ A C − B C < 3 λ ⇔ 2 λ ≤ A B 2 + B C 2 − B C < 3 λ ⇔ 2 λ ≤ A B 2 + 3 4 A B 2 − 3 4 A B < 3 λ ⇔ 2 λ ≤ A B 2 + 3 4 A B 2 − 3 4 A B < 3 λ ⇔ 2 λ ≤ A B 2 < 3 λ ⇔ 4 ≤ A B λ < 6
Vậy A B λ (phần nguyên của A B λ ) giá trị lớn nhất là 5
Suy ra, số cực đại tối đa trên AB là 2 A B λ + 1 = 11 đ i ể m

Đáp án C
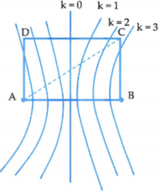
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3.
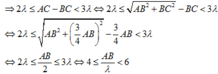
Vậy A B λ (phần nguyên của A B λ ) nhận giá trị lớn nhất là 5.
Suy ra, số cực đại tối đa trên AB là 2 A B λ +1=11 điểm.

Đáp án D
Chu kỳ sóng T = 2 π / ω = 0,1 s
Vì M dao động cùng pha với A nên M A = k λ = k . v . T ⇔ v = M A k T = 1,4 k với k ∈ ℤ
Mặt khác 0,19 m / s < v < 0,22 m / s ⇔ 0,19 < 1,4 k < 0,22
⇒ 6,36 ≤ k ≤ 7,36 ⇒ k = 7 ⇒ v = 0,2 m / s
Bước sóng λ = v . T = 0,02 m = 2 c m . Suy ra A B λ = 10
Vậy số điểm dao động với biên độ cực tiểu trên AB là 2 A B λ = 20 đ i ể m




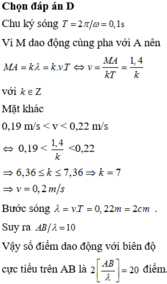



Chọn A.
Ba nguồn kết hợp dao động ngược pha A và B
⇒ Những điểm nằm trên đường trung trực của đoạn AB trên mặt nước sẽ dao động với biên độ cực tiểu.