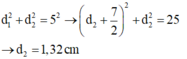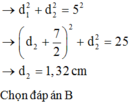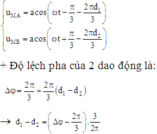Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Ta có hai nguồn dao động ngược pha nên ta có điểm P dao động với biên độ cực đại khi d 1 - d 2 = k + 1 2 λ
S 1 M N S 2 là hình vuông với S 1 S 2 = 30 ⇒ S 2 M = 30 2
Tại S2 ta có Số điểm dao động với biên độ cực đại trên S 2 M ứng với k thuộc [-4,9]→Có 14 điểm
Đáp án C
Ta có ω = 40π → f = 20 Hz → Bước sóng λ = v/f = 40/20 = 2 cm.
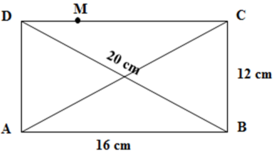
Gọi M là điểm bất kì thuộc CD dao động với biên độ cực đại.
→ MA – MB = (k + 0,5)λ (do hai nguồn ngược pha)
Mà DA – DB ≤ MA – MB ≤ CA – CB và DB = AB 2 + BC 2 = 20 cm .
→ 12 – 20 ≤ (k + 0,5).2 ≤ 20 – 12 ↔ -4 ≤ k + 0,5 ≤ 4 → -4,5 ≤ k ≤ 3,5.
Có 8 giá trị k nguyên thỏa mãn điều kiện → có 8 điểm dao động với biên độ cực đại trên đoạn CD.
Đáp án C
+ Điều kiện để có cực đại giao thoa với hai nguồn ngược pha
∆ d = d 2 - d 1 = ( k + 0 , 5 ) λ .
Với khoảng giá trị của ∆ d :
0 - 14 , 5 cm < ∆ d < 10 , 875 - 3 , 625 cm → - 7 , 75 ≤ k ≤ 3 , 125 .
→ Có 11 điểm dao động với biên độ cực đại.
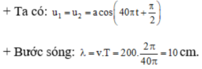
+ Kết hợp với:
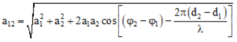
+ Biên độ cực tiểu:
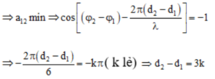
Mặt khác:
vì k lẻ nên có hai giá trị thỏa mãn
Có 2 điểm dao dộng với biên độ cực tiểu trên CD
Chọn C
Đáp án C
+ Hai nguồn ngược pha, có bước sóng: λ = v f = 40 20 = 2
+ A P = 3 4 A B = 10 , 875 ; B P = 1 4 A B = 3 , 625 c m
+ Số điểm dao động với biên độ cực đại trên đoạn AP thỏa mãn biểu thức sau:
− A B < k + 1 2 λ ≤ A P − B P ⇔ − 14 , 5 < k + 1 2 2 ≤ 7 , 25
→ 7 , 75 < k < 3 , 125 → k = − 7 ; − 6 ; − 8 ; − 4 ; ± 3 ; ± 2 ; ± 1 ; 0
→ Vậy có 11 điểm dao động với biên độ cực đại trên AP
- Phương trình dao động của M đối với 2 nguồn là:
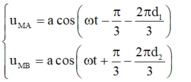
- Độ lệch pha của 2 dao động là:
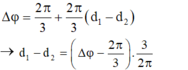
- M dao động với biên độ cực tiểu nên ta có:
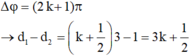
- Số điểm dao động với biên độ cực tiểu trên AB là:
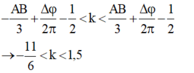
- Mà M cách B đoạn nhỏ nhất:
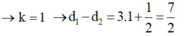
- Lại có:
