Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng của sóng : λ = v/f = 120/20 = 6cm. S 1 S 2 = 18cm = 6 λ /2. Trừ hai điểm S 1 , S 2 thì trên đoạn thẳng S 1 S 2 có 5 điểm, tại đó mặt nước dao động mạnh nhất.
Vậy : "Nếu không tính gợn sóng thẳng trùng với đường trung trực của S 1 S 2 thì có 4 gợn sóng hình hypebol".

Bước sóng λ = v/f = 80/50 = 1,6cm
Đỉnh của hai đường hypebol, tại đó chất lỏng dao động mạnh nhất, cách nhau : i = λ /2 = 1,6/2 = 0,8cm
Vì tại trung điểm của S 1 S 2 có một vân cực đại (đường thẳng) nên số vân cực đại nằm trên một nửa đoạn S 1 S 2 là :
N' = [6/0,8] = 7 vân
Kí hiệu [ ] chỉ phần nguyên.
Số đường hypebol (quỹ tích các điểm dao động cực đại) N = 2N' = 14. Nếu coi đường trung trực của S 1 S 2 như một hypebol đặc biệt thì số vân cực đại sẽ là 15.

Giữa đỉnh của hypebol số 1 và đỉnh của hypebol số 12 có 11 khoảng vân.
Vậy i = 22/11 = 2cm = λ /2 ⇒ λ = 4cm
Tốc độ truyền sóng : v = λ f = 20.4 = 80cm/s

Khi hệ vân giao thoa đã ổn định thì trung điểm I của S 1 S 2 lại luôn luôn là cực đại giao thoa. Do đó, ta phải có :
S 1 I = S 2 I = k λ /2 + λ /4 = (2k + 1) λ /4
S 1 S 2 = 2 S 1 I = (2k + 1) λ /2
Ban đầu ta đã có : S 1 S 2 = 8cm = 10 λ = 20 λ /2
Vậy chỉ cần tăng khoảng cách S 1 , S 2 thêm λ /2 tức là 0,4 cm.
Khi đó nếu không kể đường trung trực của S 1 S 2 thì có 20 gợn sóng hình hypebol (vì gợn sóng là quỹ tích những điểm dao động mạnh hơn cả).

Đáp án A
λ
=
v
f
=
3
c
m
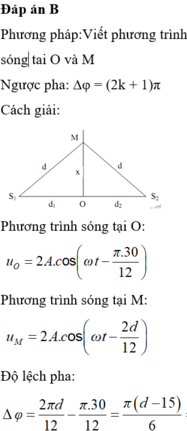
Điểm nằm trên đường tròn gần trung điểm nhất sẽ ở trên đường dao thoa cực đại ứng với k = 1 hoặc k = -1 (2 trường hợp trường hợp nào gần hơn thì lấy)
Gọi I là trung điểm của
S
1
S
2
•
k
=
1
:
S
2
M
-
S
1
M
=
1
λ
⇔
S
2
M
-
30
=
3
⇔
S
2
M
=
33
c
m
Gọi N là hình chiếu của M lên
S
1
S
2
, IN chính là khoảng cách từ M đến trung trực
S
1
S
2
:
S 1 M 2 - S 1 N 2 = M N 2 = S 2 M 2 - S 2 N 2 ⇔ S 2 N 2 - S 1 N 2 = S 2 M 2 - S 1 M 2
Ta có :
33
2
-
30
2
=
189
Cộng với
•
S
2
N
+
S
1
N
=
S
1
S
2
=
30
⇒
S
2
N
=
18
.
15
c
m
⇒
I
N
=
3
.
15
c
m
k = -1 : Tương tự ta có S 2 M = 27 c m
Ta có
S 2 N 2 - S 1 N 2 = S 2 M 2 - S 1 M 2 = 27 2 - 30 2 = - 171
S 2 N - S 1 N = 30 c m ⇒ S 1 N = 17 . 85 ⇒ I N = 2 , 85 c m
Vậy khoảng cách ngắn nhất là 2,85 cm

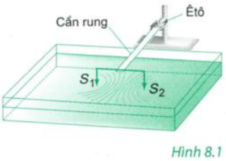
Đáp án B
+ Xét tỉ số d 2 - d 1 λ = 3
→ Vậy ban đầu điểm M nằm trên cực đại thứ 3 ⇒ h = 2 , 52 cm x = 3 , 36 cm
+ Dịch chuyển S2 ra xa một đoạn ∆ d , để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4.
Ta có d 2 ' - d 1 = 3 , 5 λ ⇒ d 2 ' = 9 , 8 cm ⇒ ∆ d = 0 , 83 cm .
Đáp án C
Khoảng cách giữa S1, S2 có 10 cực tiểu liên tiếp là nên 9 λ 2
9 λ 2 = 18 ⇒ λ = 4 ( c m ) ⇒ v = λ f = 100 ( c m / s )