Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda=\frac{v}{f}=\frac{12}{5}=2.4cm\)
Số điểm cực đại trong đoạn MN chính là số giá trị k thỏa mãn \(NO_{2}-NO_{1} \leq d_{2}-d_{1} \leq MO_{2}-MO_{1} \Rightarrow -12 \leq (k+ \frac{\triangle \phi}{2\pi})\lambda \leq 7\\ \Rightarrow -5.25 \leq k \leq 2.7 \)
=> k = -5,-4,-3,-2,-1,0,1,2. Có 8 vân cực đại trong đoạn MN.
Số điểm cực tiểu trong đoạn MN:
\(NO_{2}-NO_{1} \leq d_{2}-d_{1} \leq MO_{2}-MO_{1} \Rightarrow -12 \leq (2k+1+ \frac{\triangle \phi}{\pi})\frac{\lambda}{2} \leq 7\\ \Rightarrow -5.75\leq k \leq 2.16\)
=>k = -5,...,0,1,2. Có 8 vân cực tiểu trong đoạn MN.

Bước sóng: \(\lambda = v.T=15.0,4=6cm\)
Ta có: \(d_2-d_1=15-21=-6cm=-\lambda\)
Suy ra M nằm trên vân giao thoa cực đại thứ 1.

Đáp án C
d 2 - d 1 = k λ → 8 c m - 3 , 5 c m = 3 λ → λ = 1 , 5 c m → v = λ f = 60 c m / s

Đáp án C
d 2 - d 1 = k λ → 8 c m - 3 , 5 c m = 3 λ → λ = 1 , 5 c m → v = λ f = 60 c m / s

Đáp án B
+ M và N cùng loại do vậy ta luôn có hiệu số:
∆ d N - ∆ d M = 2 λ ⇒ λ = 3 cm.
+Xét tỉ số S 1 P - S 2 P λ = - 6 , 9 có 13 điểm cực đại trên PQ


Đáp án B
+ Xét tỉ số d 2 - d 1 λ = 3
→ Vậy ban đầu điểm M nằm trên cực đại thứ 3 ⇒ h = 2 , 52 cm x = 3 , 36 cm
+ Dịch chuyển S2 ra xa một đoạn ∆ d , để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4.
Ta có d 2 ' - d 1 = 3 , 5 λ ⇒ d 2 ' = 9 , 8 cm ⇒ ∆ d = 0 , 83 cm .

Đáp án A
Bước sóng: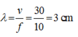
Số vân cực đại và cực tiểu thỏa mãn:
Như vậy có 5 vân cực đại và 6 vân cực tiểu.