Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Link đây bạn xem thử
https://www.google.com/search?sxsrf=ALeKk000ftx557H7QV3mBjlHBDDRymSGFQ%3A1586183472602&ei=MD2LXoS4JM3EmAXR5YT4Dg&q=Cho+ba+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+y+%3D+-x+%2B+1%2C+y+%3D+x+%2B+1+v%C3%A0+y+%3D+-1.+V%E1%BA%BD+ba+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+%C4%91%C3%A3+cho+tr%C3%AAn+c%C3%B9ng+m%E1%BB%99t+h%E1%BB%87+tr%E1%BB%A5c+t%E1%BB%8Da+%C4%91%E1%BB%99+Oxy.+G%E1%BB%8Di+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+y+%3D+-x+%2B+1+v%C3%A0+y+%3D+x+%2B+1+l%C3%A0+A%2C+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+y+%3D+-1+v%E1%BB%9Bi+hai+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+y+%3D+-x+%2B+1+v%C3%A0+y+%3D+x+%2B+1+theo+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+B+v%C3%A0+C.+T%C3%ACm+t%E1%BB%8Da+%C4%91%E1%BB%99+c%C3%A1c+%C4%91i%E1%BB%83m+A%2C+B%2C+C.+Tam+gi%C3%A1c+ABC+l%C3%A0+tam+gi%C3%A1c+g%C3%AC%3F+T%C3%ADnh+di%E1%BB%87n+t%C3%ADch+tam+gi%C3%A1c+ABC
Học tốt

a, HS Tự làm
b, Tìm được C(–2; –3) là tọa độ giao điểm của d 1 và d 2
c, Kẻ OH ⊥ AB (CH ⊥ Ox)
S A B C = 1 2 C H . A B = 9 4 (đvdt)

a/ Bạn tự vẽ
b/ Ta lập pt hoành độ giao điểm :
(d1) giao với (d2) : \(-x-5=\frac{1}{4}x\Leftrightarrow x=-4\) thay vào (d1) được y = -1
Vậy A(-4;-1) . Tương tự ta tìm được điểm B(-1;-4)
c/ Ta có : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(-1+4\right)^2+\left(-4+1\right)^2}=3\sqrt{2}\)
\(OA=\sqrt{x_A^2+y_A^2}=\sqrt{4^2+1^2}=\sqrt{17}\) ; \(OB=\sqrt{x_B^2+y_B^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
=> OAB là tam giác cân
d/ Gọi OH là đường cao hạ từ O xuống AB (H thuộc AB)
Vì tam giác OAB cân tại O nên AH = HB = 1/2AB = \(\frac{3\sqrt{2}}{2}\)
\(OH=\sqrt{OA^2-BH^2}=\sqrt{17-\left(\frac{3\sqrt{2}}{2}\right)^2}=\frac{5\sqrt{2}}{2}\)
\(S_{ABC}=\frac{1}{2}AB.OH=\frac{1}{2}.3\sqrt{2}.\frac{5\sqrt{2}}{2}=\frac{15}{2}\)

(d1): y = 1/2x + 2
và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
(d1) là đường thẳng đi qua hai điểm (0; 2) và (-4; 0)
(d2) là đường thẳng đi qua hai điểm (0; 2) và (2;0)
2. Tính chu vi và diện tích của tam giác ABC
(d1) và (d2) cùng cắt nhau tại một điểm trên trục tung có tung độ bằng 2
Áp dụng định lý Pi ta go cho các tam giác AOC và BOC vuông ở O ta được:
\(AC=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}\)
\(BC=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
Chu vi tam giác ABC : AC + BC + AB= 2√5 + 2√2 + 6
≈ 13,30
Diện tích tam giác ABC
\(\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6CM^2\)
NHÉ THAK NHÌU

b: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}3x=-x+4\\y=3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

a: 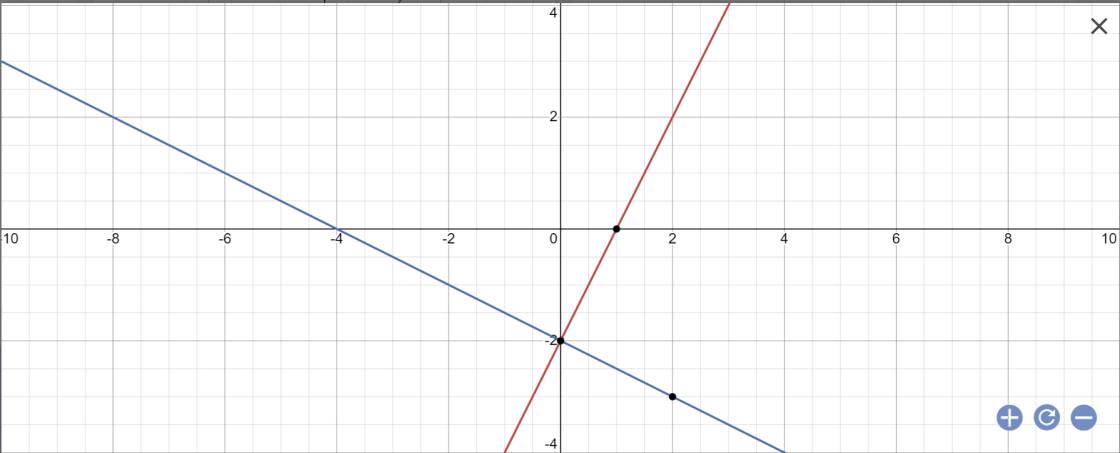
b: Tọa độ A là:
2x-2=-1/2x-2 và y=2x-2
=>x=0 và y=-2
Tọa độ B là:
y=0 và 2x-2=0
=>x=1 và y=0
Tọa độ C là:
y=0 và -1/2x-2=0
=>x=-4; y=0
i: A(0;-2); B(1;0); C(-4;0)
\(\overrightarrow{AB}=\left(1;2\right);\overrightarrow{AC}=\left(-4;2\right)\)
Vì 1*(-4)+2*2=0
nên ΔABC vuông tại A
ii: \(AB=\sqrt{1^2+2^2}=\sqrt{5}\)
\(AC=\sqrt{\left(-4\right)^2+2^2}=2\sqrt{5}\)
\(BC=\sqrt{5+20}=5\left(cm\right)\)
\(C_{ABC}=AB+AC+BC=5+3\sqrt{5}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{5}=5\left(cm^2\right)\)