Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách

Chọn A
|
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
| 1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
Gọi Ω là biến cố “xếp quyển sách lên kệ sách một cách tùy ý”
=> n( Ω ) = 14!
A là biến cố “xếp 14 cuốn sách lên kệ sách sao cho hai cuốn sách cùng môn không ở cạnh nhau”.
- Xếp quyển sách Tiếng Anh vào kệ có 7! cách.
- quyển sách Tiếng Anh tạo ra 8 chỗ trống (gồm 6 chỗ trống ở giữa và 2 chỗ trống trước sau).
Đánh số từ 1 đến 8, từ trái sang phải cho các chỗ trống. Khi đó ta xét các trường hợp:
TH1: Xếp sách Văn hoặc Toán vào vị trí từ 1 đến 7 có 7! cách.
TH2: Xếp sách Văn hoặc Toán vào vị trí từ 2 đến 8 có 7! cách.
TH3: Xếp cặp sách Văn – Toán chung vào ngăn, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại. Ta có:
+ Số cách chọn cặp sách Văn – Toán: 3.4 cách.
+ Vị trí 2 cuốn sách trong cặp sách: 2! cách.
+ Xếp các sách còn lại vào các ngăn 3,4,5,6,7 có 5! cách
Vậy ta có số cách xếp 1 cặp sách Văn – Toán chung vào ngăn 2, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại là 3.4.2!.5! cách.
Tương tự cho xếp cặp sách Văn – Toán lần lượt vào các ngăn 3,4,5,6,7
Số trường hợp thuận lợi của biến cố là ![]()
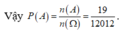

Có 3 môn học nên có 3! Cách xếp sách theo môn Ứng với mỗi cách xếp theo môn có 5!cách xếp toán,4! Cách xếp hóa và 3! Cách xếp sách lí. Vậy số cách xếp sách là : 3!5!4!3!cách
Chọn C

Đáp án A.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5!.2! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240 . A 4 3 . 3 10 ! = 1 210 .

Xếp theo thứ tự: ngữ văn- toán- ngữ văn- toán- ngữ văn- toán-ngữ văn-toán- ngữ văn. Vậy có 5.4.4.3.3.2.2.1=2880 cách
Chọn B

Để sắp xếp số sách đó lên kệ và thỏa mãn đầu bài ta cần làm hai công việc sau:
Đầu tiên; đặt 3 nhóm sách ( toán; văn; anh) lên kệ có 3!=6 cách.
Sau đó; trong mỗi nhóm ta có thể thay đổi cách xếp các quyển sách với nhau:
Nhóm toán có 4!=24 cách.
Nhóm văn có 2!=2 cách.
Nhóm anh có 6!=720 cách.
Theo quy tắc nhân có : 6.24.2.720=207360 cách.
Chọn B.
c. Số cách chọn 2 quyển sách khác môn học là: 5×6+5×8+6×8=118
Chọn C