


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




có sđ AB = sđ BC = sđ CD
mà BIC = 1/2 ( sđ AD - sđ BC ) =1/2 ( sđ BD - sđ AB -sđ BC )
BKD = 1/2 ( sđ BD - sđ BC-sđ CD )
nên BIC=BKD
b,KBC = CDB ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung CD)
mà CDB = CBD ( BC = CD )
nên KBC = CBD => BC là tia pg của KBD
A)
Vì góc BIC có đỉnh nằm ngoài đường tròn
nên: góc BIC = \(\dfrac{sđAD-sđBC}{2}\)
Mà: sđAD = \(\dfrac{sđBD+sđAB}{2}\) ; sđBC = sđ AB = sđCD
=> góc BIC = \(\dfrac{sđBD+sđAB-sđAB}{2}\) = \(\dfrac{sđBD}{2}\) (1)
Ta có: góc BKD = \(\dfrac{sđBD}{2}\) (2)
từ (1) và (2) => góc BIC = góc BKD
B)
Vì góc KBC và góc BDC cùng chắn cung BC
=> góc KBC = góc BDC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung )
Ta có: sđBC = sđCD (gt)
nên: góc BDC = góc DBC (hai góc nội tiếp chắn hai cung bằng nhau)
Vậy góc KBC = góc DBC (cùng bằng góc BDC)
hay: BC là tia phân giác của góc DBK

a) vì AD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)\(\Rightarrow\)D là điểm chính giữa BC
\(\Rightarrow OD\perp BC\)
Mà \(DE\perp OD\)
\(\Rightarrow BC//DE\)
b) Ta có : \(\widehat{DAC}=\widehat{DCI}=\frac{1}{2}sđ\widebat{CD}\)
\(\Rightarrow\widehat{KAD}=\widehat{KCI}\)
suy ra tứ giác ACIK nội tiếp
c) OD cắt BC tại H
Dễ thấy H là trung điểm BC nên HC = \(\frac{BC}{2}=\frac{\sqrt{3}}{2}R\)
Xét \(\Delta OHC\)vuông tại H có :
\(HC=OC.\sin\widehat{HOC}\Rightarrow\sin\widehat{HOC}=\frac{HC}{OC}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{HOC}=60^o\)
\(\Rightarrow\widehat{BOC}=120^o\)
\(\Rightarrow\widebat{BC}=120^o\)
P/s : câu cuối là tính số đo cung nhỏ BC mà sao có cái theo R. mình ko hiểu. thôi thì bạn cứ xem đi nha.

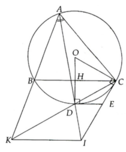
a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR


d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm