Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Bn là tập hợp các số nguyên chia hết cho n. Bm là tập hợp các số nguyên chia hết cho m. Để Bn ⊂ Bm thì các phần tử thuộc Bn cũng thuộc Bm, tức là n chia hết cho m hay n là bội số của m.

Đáp án: A
M là tập hợp các số nguyên chia hết cho 10. N là tập hợp các số nguyên chia hết cho 2. Các số chia hết cho 10 chắc chắn phải chia hết cho 2, ngược lại các số chia hết cho 2 thì chưa chắc chia hết cho 10. Do đó M ⊂ N => M ∩ N => A đúng, C sai.
P = {1; 3; 5; 15}; Q = {1; 2; 3; 5; 6; 10; 15; 30}. Do đó P ⊂ Q => P ∩ Q = P => B, D sai

Đáp án: C
M là tập hợp các số nguyên chia hết cho 2. N là tập hợp các số nguyên chia hết cho 6. Các số chia hết cho 6 chắc chắn phải chia hết cho 2, ngược lại các số chia hết cho 2 thì chưa chắc chia hết cho 6. Do đó N ⊂ M => M ∩ N = N
=> A sai, C đúng.
P = {1; 2}; Q = {1; 2; 3; 6}. Do đó P ⊂ Q => P ∩ Q = P => B, D sai.

a: \(B_2\cup B_4=B_4\)
\(B_4\cap B_6=B\left(12\right)\)
\(B_5\cap B_7=B\left(35\right)\)
b: \(B_n\subset B_m\) khi n là ước của m
\(B_n\cap B_m=B_{m\cdot n}\) khi ƯCLN(m,n)=1



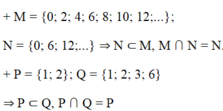
Câu trả lời của ConnanMTM không đúng nhé. Khẳng định B không đúng chẳng hạn với n = 4, m = 2 không xảy ra
\(B_n\cap B_m=B_{nm}\). Thật vậy, với n = 4, m = 2 thì nm = 8 và
\(B_n=B_4=\left\{0;\pm4;\pm8;...\right\}\)
\(B_m=B_2=\left\{0;\pm2;\pm4;\pm6;\pm8,...\right\}\) suy ra \(B_n\subset B_m\) và \(B_n\cap B_m=B_n=\left\{0;\pm4;\pm8;...\right\}\)
\(B_{nm}=B_8=\left\{0;\pm8;\pm16;...\right\}\). Do đó trường hơp này không xảy ra \(B_n\cap B_m=B_{nm}\). (đpcm)
Câu trả lời đúng là C.
B. n là bội số của m nha bn !!!
Chúc bn hok tốt !!!!!