Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
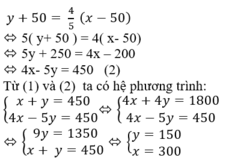
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
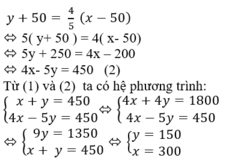
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Sau khi chuyển thì tổng số sách không đổi.
Sau khi chuyển nếu số sách ở ngăn thứ hai là \(4\)phần thì số sách ở ngăn thứ nhât là \(5\)phần.
Tổng số phần bằng nhau là:
\(4+5=9\)(phần)
Sau khi chuyển số sách ở ngăn thứ hai là:
\(450\div9\times4=200\)(cuốn)
Số sách ở ngăn thứ hai lúc đầu là:
\(200-50=150\)(cuốn)
Số sách ở ngăn thứ nhất lúc đầu là:
\(450-150=300\)(cuốn)
Sau khi chuyển thì tổng số sách hai ngăn không thay đổi.
Ta có sơ đồ :
Ngăn thứ nhất : |-----|-----|-----|-----|-----|
Ngăn thứ hai : |-----|-----|-----|-----|
Tổng số phần bằng nhau là :
4 + 5 = 9 ( phần )
Ngăn thứ hai chứa số sách lúc đầu là :
450 : 9 × 4 - 50 = 150 ( cuốn )
Ngăn thứ nhất chứa số sách lúc đầu là :
450 - 150 = 300 ( cuốn )
Đáp số : Ngăn thứ hai : 150 cuốn sách
Ngăn thứ nhất : 300 cuốn sách

Gọi : x là số sách ở ngăn 1
Gọi : y là số sách ở ngăn 2
__ vì Lúc đầu số sách ngăn 1 bằng 7/3 số sách ngăn 2. nên ta có phương trình :
\(x=\frac{7}{3}y\)
\(< =>\frac{3x}{3}=\frac{7y}{3}\)
\(< =>3x=7y\)
\(< =>3x-7y=0\) \(\left(1\right)\)
__ vì Người ta chuyển vào mỗi ngăn 40 quyển .Khi đó số sách ngăn 2 bằng 17/29 số sách ngăn 1. nên ta có phương trình :
\(\frac{17}{29}\left(x+40\right)=y+40\)
\(< =>\frac{17.\left(x+40\right)}{29}=\frac{29.\left(y+40\right)}{29}\)
\(< =>17x+680=29y+1160\)
\(< =>17x-29y=480\) \(\left(2\right)\)
Từ ( 1 ) vả ( 2 ) ta có hệ phương trình :
\(\hept{\begin{cases}3x-7y=0\\17x-29y=480\end{cases}}\)
\(< =>\hept{\begin{cases}51x-119y=0\\-51x+87y=-1440\end{cases}}\)
\(< =>\hept{\begin{cases}-32y=-1440\\3x-7y=0\end{cases}}\)
\(< =>\hept{\begin{cases}y=45\\3x-7.45=0\end{cases}}\)
\(< =>\hept{\begin{cases}y=45\\x=\frac{315}{3}\end{cases}}\)
\(< =>\hept{\begin{cases}y=45\\x=105\end{cases}}\)
SỔ SÁCH CỦA CẢ 2 NGÂN LÚC NÀY LÀ :
\(x+40+y+40=105+40+45+40=230\)
OK CHÚC BẠN HC TỐT !!!!!

Gọi x (cuốn) là số cuốn sách ở giá thứ nhất. ĐK: 450>x>50; \(x\in N\)
--> 450-x (cuốn) là số cuốn sách ở giá thứ hai
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách của giá thứ nhất lúc này là x-50 ( cuốn) và giá thứ hai là 500-x ( cuốn)
Khi đó số sách ở giá thứ hai bằng 4/5 số sách ở giá thứ nhất nên ta có pt:
\(500-x=\dfrac{4}{5}\left(x-50\right)\)
\(\Leftrightarrow500-x=\dfrac{4}{5}x-40\Leftrightarrow\dfrac{9}{5}x=540\Leftrightarrow x=300\)(tm)
Vậy số sách ở giá thứ nhất là 300 cuốn ; số sách ở giá thứ hai là 150 cuốn