Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số hs lớp 9A là x => số hsg của lớp 9A là \(\frac{x.60}{100}\)
Gọi số hs lớp 9B là y => số hsg của lớp 9b là \(\frac{y.75}{100}\)
=> Ta có pt (1) \(\frac{60x}{100}+\frac{75y}{100}=51\Leftrightarrow12x+15y=1020\)
Ta có hệ PT
\(\hept{\begin{cases}x+y=76\\12x+15y=1020\end{cases}}\)
Giải hệ PT trên
Gọi a(bạn) là số học sinh của lớp 9A(Điều kiện: \(a\in Z^+\))
Gọi b(bạn) là số học sinh của lớp 9B(Điều kiện: \(b\in Z^+\))
Vì khi chuyển ba học sinh từ 9A sang lớp 9B thì số học sinh hai lớp bằng nhau nên ta có phương trình:
\(a-3=b+3\)
\(\Leftrightarrow a-3-b-3=0\)
\(\Leftrightarrow a-b-6=0\)
hay a-b=6(1)
Vì khi chuyển 5 học sinh từ 9B sang lớp 9A thì số học sinh lớp 9B bằng \(\dfrac{11}{19}\)số học sinh lớp 9A nên ta có phương trình:
\(b-5=\dfrac{11}{19}\cdot\left(a+5\right)\)
\(\Leftrightarrow b-5-\dfrac{11}{19}a-\dfrac{55}{19}=0\)
\(\Leftrightarrow\dfrac{-11}{19}a+b=\dfrac{150}{19}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a-b=6\\-\dfrac{11}{19}a+b=\dfrac{150}{19}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{19}a=\dfrac{264}{19}\\a-b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=33\left(nhận\right)\\b=a-6=33-6=27\left(nhận\right)\end{matrix}\right.\)
Vậy: Số học sinh lớp 9A là 33 bạn
Số học sinh lớp 9B là 27 bạn
tăng thêm 2 học sinh vào lớp 9a, bớt 3 học sinh lớp 9b thì học sinh hai lớp bằng nhau=> lớp 9a ít hơn lớp 9b :
2+3=5 học sinh
số học sinh lớp 9a=(101-5):2=48
số học sinh lớp 9b=48+5=53
Đáp án B
Gọi x, y lần lượt là số học sinh của lớp 9A và lớp 9B (x, y ∈ N*; x, y < 82)
Tổng số học sinh của hai lớp là 82 ⇒ x + y = 82 (1)
Mỗi học sinh lớp 9A và 9B lần lượt trồng được 3 cây và 4 cây nên tổng số cây hai lớp trồng là 3x + 4y (cây). Theo bài ra ta có 3x + 4y = 288 (2)
Từ (1) và (2) ta có hệ phương trình:
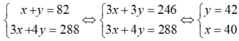(thỏa mãn)
Vậy số học sinh lớp 9A và 9B lần lượt là 40 và 42.
