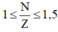Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Trong nguyên tử thì tỉ số N/Z ≥ 1 và N/Z ≤ 1,5
- Trong nguyên tử số proton bằng số electron.
Theo đầu bài tổng 3 loại hạt là 13. Ta có thể biện luận như sau :
+ Nếu số p = số e = 3 thì số n = 13 - (3 + 3) = 7.
Tỉ số N/Z = 7/3 = 2,3 > 1,5 (loại)
+ Nếu số p = số e = 4 thì số n = 13 - (4 + 4) = 5.
Tỉ số N/Z = 5/4 = 1,25 (phù hợp)
+ Nếu số p = số e = 5 thì số n = 13 - (5 + 5) = 3.
Tỉ số N/Z = 3/5 = 0,6 < 1 (loại)
Vậy nguyên tử đó có Z = 4. Đó là beri (Be).
Nguyên tử khối của nguyên tố đó là : 4 + 5 = 9 đvC.
Cấu hình electron nguyên tử : 1 s 2 2 s 2

Ta có: \(1\le\dfrac{N}{Z}\le1,5\)
\(\Rightarrow Z\le N\le1,5Z\)
\(\Rightarrow3Z\le2Z+N\le3,5Z\)
Vậy ta có : \(3Z\le24\le3,5Z\)
=> \(6,86\le Z\le8\)
=>\(\left[{}\begin{matrix}Z=7\left(N\right)\\Z=8\left(O\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}N=10\\N=8\end{matrix}\right.\)
Mà theo đề bài : \(1\le\dfrac{N}{Z}\le1,5\)
=> Chỉ có O thỏa mãn
=> Z là O , số P= số E =8 , N=8
b) Cấu hình E: 1s22s22p4