K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2021
28. R1 nt R2( y a, ban tu ve)
b,\(\Rightarrow I1=I2=\dfrac{U}{R1+R2}=\dfrac{18}{30+60}=0,2A=Ia\)=> so chi ampe ke la 0,2A
\(\Rightarrow\left\{{}\begin{matrix}Uv1=I1R1=6V\\Uv2=I2R2=12V\end{matrix}\right.\)
B
28 tháng 11 2021
Tóm tắt:
\(R_1=8\Omega\)
\(R_2=12\Omega\)
\(R_3=4\Omega\)
\(U=48V\)
_______
Giải:
Điện trở tương đương của mạch:
\(R_{tđ}=R_1+R_2+R_3=8+12+4=24\Omega\)
Cường độ dòng điện qua mạch chính:
\(I=I_1=I_2=I_3=\dfrac{U}{R_{tđ}}=\dfrac{48}{24}=2A\)
Hiệu điện thế \(R_2\)
\(U_2=I.R_2=2.12=24V\)
N
6 tháng 11 2021
Tóm tắt:
R1 // R2
\(R1=40\Omega\)
\(R2=60\Omega\)
\(U=12V\)
a. R = ?\(\Omega\)
b. I, I1, I2 = ?A
GIẢI:
a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{40.60}{40+60}=24\Omega\)
b. \(U=U1=U2=12V\left(R1\backslash\backslash\mathbb{R}2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=12:40=0,3A\\I2=U2:R2=12:60=0,2A\end{matrix}\right.\)
6 tháng 11 2021
Tóm tắt: \(U_{AB}=12V;R_1=40\Omega;R_2=60\Omega\)
a)\(R_{tđ}=?\)
b)\(I_1=?;I_2=?\)
Bài giải:
a)Điện trở tương đương:\(R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{40\cdot60}{40+60}=24\Omega\)
b)\(U_1=U_2=12V\)
\(I_1=\dfrac{12}{40}=0,3A;I_2=\dfrac{12}{60}=0,2A\)
6 tháng 11 2021
Điện trở dây đẫn phụ thuộc vào chiều dài dây và tiết diện dây.
Điện trở dây:
\(R=\rho\cdot\dfrac{l}{S}=1,7\cdot10^{-8}\cdot\dfrac{100}{1\cdot10^{-6}}=1,7\Omega\)
tóm tắt giúp mik vs
24 tháng 12 2021
Bài 3:
Điện trở của dây là:
\(R=\rho\dfrac{l}{S}=0,5.10^{-6}.\dfrac{16}{0,5.10^{-6}}=16\left(\Omega\right)\)
Nhiệt lượng nước tỏa vào:
\(Q_{tỏa}=A=P.t=\dfrac{U^2}{R}.t=\dfrac{220^2}{16}.20.60=3630000\left(J\right)=\dfrac{121}{120}\left(kWh\right)\)
có tóm tắt nha
N
15 tháng 11 2021
Tóm tắt:
\(R1=9\Omega\)
\(R2=15\Omega\)
\(R3=10\Omega\)
a. \(R=?\Omega\)
b. \(I3=0,4A\Rightarrow I1,I2=?A\)
GIẢI:
a. \(R=R1+\dfrac{R2\cdot R3}{R2+R3}=9+\dfrac{15\cdot10}{15+10}=15\Omega\)
b. \(U23=U2=U3=I3\cdot R3=0,3\cdot10=3V\left(R2//R3\right)\)
\(I2=U2:R2=3:15=0,2A\)
\(I=I1=I23=I2+I3=0,3+0,2=0,5A\left(R1ntR23\right)\)
6 tháng 11 2021
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}==\dfrac{40.60}{40+60}=24\left(\Omega\right)\)
\(U=U_1=U_2=12V\)
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{12}{40}=0,3\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{60}=0,2\left(A\right)\end{matrix}\right.\)
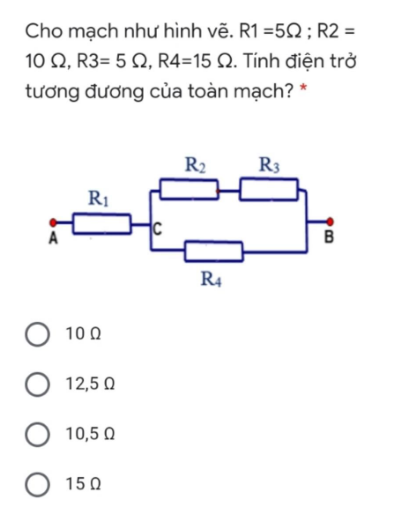
Tóm tắt:
\(R_1=5\Omega\)
\(R_2=10\Omega\)
\(R_3=5\Omega\)
\(R_4=15\Omega\)
Giải:
Điện trở của mạnh rẽ \(R_{234}\)
\(R_{234}=\dfrac{\left(R_2+R_3\right).R_4}{R_1+R_2+R_3}=\dfrac{\left(5+10\right).15}{10+5+15}=7,5\Omega\)
Điện trở tương đương của mạch:
\(R_{tđ}=R_1+R_{234}=5+7,5=12,5\Omega\)
Cảm ơn ah