
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=-\dfrac{144}{9}x^2yz^2=-16x^2yz^2\)
b: \(B=\dfrac{4}{9}x^6y^2\cdot\dfrac{-9}{10}x^4y^2z=-\dfrac{2}{25}x^{10}y^4z\)
c: \(C=\dfrac{-9}{16}\cdot\dfrac{4}{3}x^3y^5=\dfrac{-3}{4}x^3y^5\)
d: \(D=x^2y^4\cdot\dfrac{-4}{5}x^2y^3=-\dfrac{4}{5}x^4y^7\)

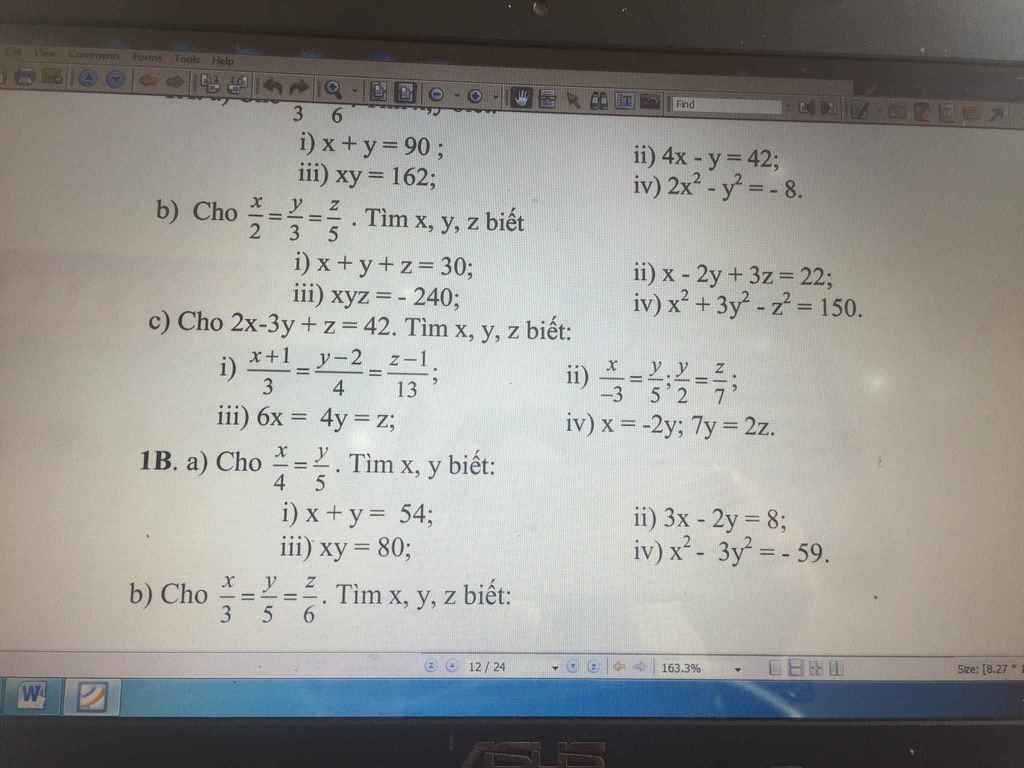
1B:
i: áp dụng tính chất của dãy tỉ só bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{x+y}{4+5}=\dfrac{54}{9}=6\)
Do đó: x=24; y=30
ii: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{3x-2y}{3\cdot4-2\cdot5}=\dfrac{8}{2}=4\)
Do đó: x=16; y=20
iii: đặt x/4=y/5=k
=>x=4k; y=5k
xy=80 nên \(20k^2=80\)
=>\(k^2=4\)
TH1: k=2
=>x=8; y=10
TH2: k=-2
=>x=-8; y=-10
a thịn ái đồ lun làm toán bất biến giữa dòng box vạn biến
a rep cmt e zesi:>

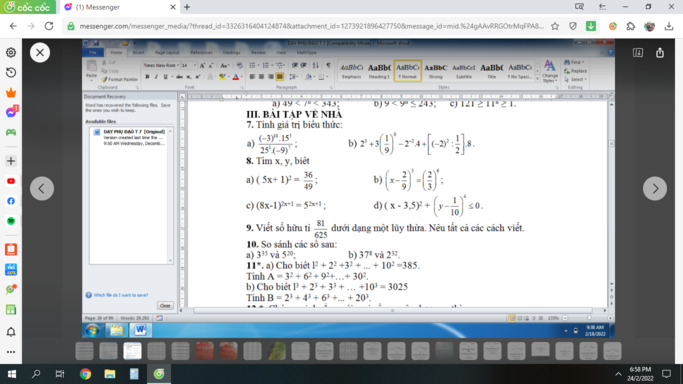
Bài 10:
a: \(3^{35}=2187^5\)
\(5^{20}=625^5\)
mà 2187>625
nên \(3^{35}>5^{20}\)
b: \(2^{32}=16^8< 37^8\)


Bài 1:
b: Xét ΔOAC và ΔOBD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔOAC=ΔOBD
Nếu cậu làm hết thì tớ sẽ thả đúng và một lượt theo dõi:3(không làm cũng không sao tớ cảm ơn)



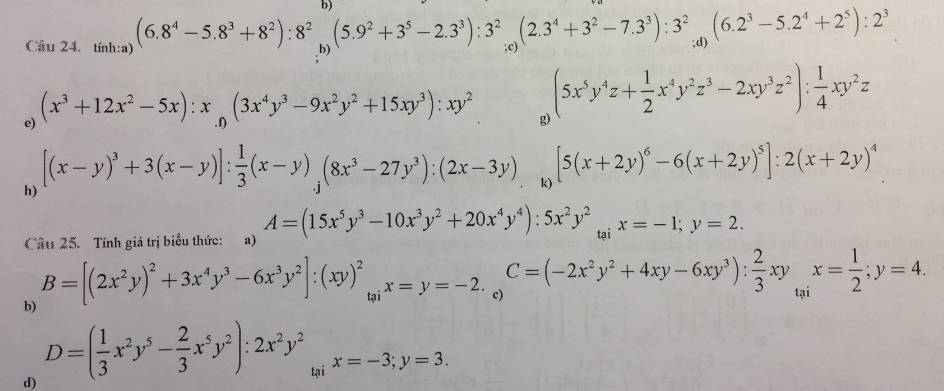
 tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé) giúp tớ bài này với ạ:3 tớ đang cần gấp
giúp tớ bài này với ạ:3 tớ đang cần gấp
