
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(0,0\left(3\right)+0,0\left(16\right)\)\(=\frac{1}{30}+\frac{16}{990}\)\(=\)\(\frac{33}{990}+\frac{16}{990}=\frac{49}{990}\)

(-4,9)+5,5+4,9+(-5,5)
=[(-4,9)+4,9]+[5,5+(-5,5)]
=(4,9-4,9)+(5,5-5,5)
=0+0
=0

d. \(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
\(\Rightarrow\left(x-2\right)\left(x+7\right)=\left(x-1\right)\left(x+4\right)\)
\(\Rightarrow x^2+5x-14=x^2+3x-4\)
\(\Rightarrow x^2+5x-x^2-3x=-4+14\)
\(\Rightarrow2x=10\) \(\Rightarrow x=\dfrac{10}{3}\) \(\Rightarrow x=5\)
\(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
⇔ \(\dfrac{\left(x-2\right)\left(x+7\right)}{\left(x-1\right)\left(x+7\right)}=\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x+7\right)\left(x-1\right)}\)
⇔ (x - 2)(x + 7) = (x + 4)(x - 1)
⇔ x2 + 7x - 2x - 14 = x2 - x + 4x - 4
⇔ x2 - x2 + 7x - 2x + x - 4x = 14 - 4
⇔ 2x = 10
⇔ x = 10/2 = 5

Đặt E(x)=0
\(\Leftrightarrow2x^2-3x=0\)
\(\Leftrightarrow x\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{3}{2}\right\}\)
Đặt E(x)=0
⇔2x2−3x=0⇔2x2−3x=0
⇔x(2x−3)=0⇔x(2x−3)=0
⇔[x=02x−3=0⇔[x=02x=3⇔⎡⎣x=0x=32⇔[x=02x−3=0⇔[x=02x=3⇔[x=0x=32
Vậy: S={0;32}

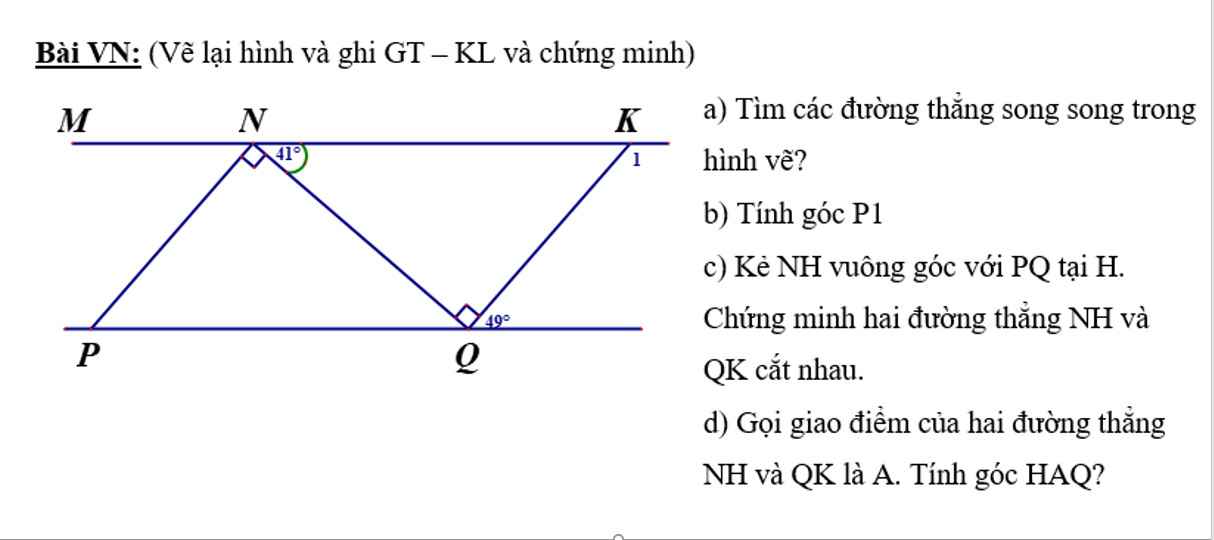
\(b,\widehat{K_1}=\widehat{KNQ}+\widehat{NQK}=41+90=131\left(góc.ngoài\right)\)
\(d,NH\perp PQ;PQ//NK\Rightarrow NH\perp NK\Rightarrow\widehat{HNK}=90\)
\(\widehat{NKQ}=180-\widehat{K_1}=180-131=49\)
\(\widehat{HAQ}=180-\widehat{HNK}-\widehat{NKQ}=180-90-49=41\)

Giải:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow70^o+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=110^o\)
Mà \(\widehat{B}-\widehat{C}=20^o\)
\(\Rightarrow\widehat{B}=\left(110^o+20^o\right):2=65^o\)
\(\Rightarrow\widehat{C}=65^o-20^o=45^o\)
Vậy ...

`P(x)=2x^3+x^2+5-3x+3x^2-2x^3-4x^2+1`
`= (2x^3-2x^3)+(x^2+3x^2-4x^2)-3x+(5+1)`
`= -3x+6`
Thay `x=0`
`P(0)=-3*0+6=6`
Thay `x=-1`
`P(-1)=(-3)*(-1)+6=3+6=9`
Thay `x=1/3`
`P(1/3)=(-3)*1/3+6=-1+6=5`

\(a,2x^3.\left(-3x^2+5\right)=2x^3.\left(-3x^2\right)+2x^3.5=-6x^{3+2}+10x^3\\ =-6x^5+10x^3\\ b,-2x^4+5x^4=\left(-2+5\right)x^4=3x^4\)

a,
\(C\left(x\right)=A\left(x\right)+B\left(x\right)=x-2x^3+3-4+2x^2+x^3-2x\\ =\left(-2x^3+x^3\right)+\left(2x^2\right)+\left(x-2x\right)+\left(3-4\right)\\ =-x^3+2x^2-x-1\)
b, Thay \(x=2\) vào \(C\left(x\right)\)
\(\Rightarrow-\left(2\right)^3+2.2^2-2-1=-3\ne0\)
\(\Rightarrow x=2\) không là nghiệm của đa thức


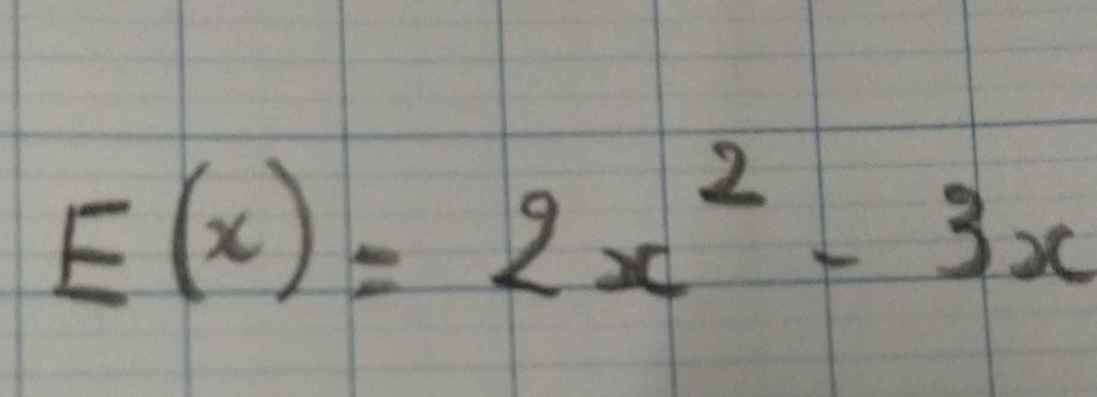
 ĐỀ BÀI CÂU B LÀ TÍNH GÓC K1 ; không phải là P1 nhé
ĐỀ BÀI CÂU B LÀ TÍNH GÓC K1 ; không phải là P1 nhé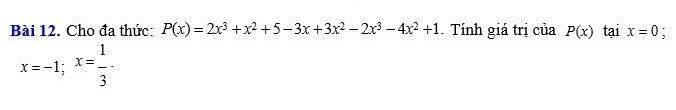
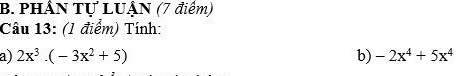

Ta có:\(P=\left(1-\dfrac{1}{1+2}\right)\left(1-\dfrac{1}{1+2+3}\right)...\left(1-\dfrac{1}{1+2+...+2014}\right)\)
\(P=\dfrac{2}{1+2}\cdot\dfrac{2+3}{1+2+3}\cdot...\cdot\dfrac{2+3+...+2014}{1+2+3+...+2014}\)
\(P=\dfrac{\dfrac{1\cdot4}{2}}{\dfrac{2\left(2+1\right)}{2}}\cdot\dfrac{\dfrac{2\left(3+2\right)}{2}}{\dfrac{3\left(3+1\right)}{2}}\cdot...\cdot\dfrac{\dfrac{2013\left(2014+2\right)}{2}}{\dfrac{2014\left(2014+1\right)}{2}}\)
\(P=\dfrac{1\cdot4}{2\cdot3}\cdot\dfrac{2\cdot5}{3\cdot4}\cdot...\cdot\dfrac{2013\cdot2016}{2014\cdot2015}\)
\(P=\dfrac{1\cdot4\cdot2\cdot5\cdot...\cdot2013\cdot2016}{2\cdot3\cdot3\cdot4\cdot...\cdot2014\cdot2015}\)
\(P=\dfrac{\left(1\cdot2\cdot...\cdot2013\right)\left(4\cdot5\cdot...\cdot2016\right)}{\left(2\cdot3\cdot\cdot...\cdot2014\right)\left(3\cdot4\cdot...\cdot2015\right)}\)
\(P=\dfrac{2016}{2014\cdot3}\)
\(P=\dfrac{336}{1007}\)
Vào đây nè bn https://olm.vn/hoi-dap/question/613645.html