
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
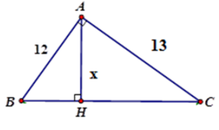
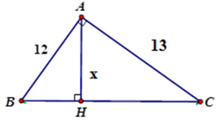
Áp dung hệ thức giữa cạnh và đường cao trong tam giác vuông ABC ta có:


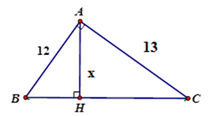
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
1 A H 2 = 1 A B 2 + 1 A C 2 ⇔ 1 A H 2 = A B 2 + A C 2 A B 2 . A C 2 ⇔ A C 2 = A B 2 . A C 2 A B 2 + A C 2
⇒ A H = A B . A C A B 2 + A C 2 = 12.13 12 2 + 13 2 ≈ 8 , 82
Vậy x ≈ 8,82
Đáp án cần chọn là: B

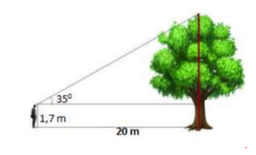
Chiều cao của cây là: h = 1,7 + 20. tan 35 0 ≈ 15,7m
Đáp án cần chọn là: B

a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:

Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x=-x+4\\y=3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
c: Gọi A,B lần lượt là giao điểm của đường thẳng y=-x+4 đến hai trục Ox, Oy
Tọa độ điểm A là: \(\left\{{}\begin{matrix}y_A=0\\4-x=0\end{matrix}\right.\Leftrightarrow A\left(4;0\right)\)
Tọa độ điểm B là: \(\left\{{}\begin{matrix}x_A=0\\y=-0+4=4\end{matrix}\right.\Leftrightarrow B\left(0;4\right)\)
\(AB=\sqrt{\left(0-4\right)^2+\left(4-0\right)^2}=4\sqrt{2}\)
Khoảng cách từ O đến đường thẳng y=-x+4 là:
\(AH=\dfrac{OA\cdot OB}{AB}=\dfrac{16}{4\sqrt{2}}=2\sqrt{2}\)
Tọa độ giao điểm là:
{3x=−x+4y=3x⇔{x=1y=3{3x=−x+4y=3x⇔{x=1y=3
c: Gọi A,B lần lượt là giao điểm của đường thẳng y=-x+4 đến hai trục Ox, Oy
Tọa độ điểm A là: {yA=04−x=0⇔A(4;0){yA=04−x=0⇔A(4;0)
Tọa độ điểm B là: {xA=0y=−0+4=4⇔B(0;4){xA=0y=−0+4=4⇔B(0;4)
AB=√(0−4)2+(4−0)2=4√2AB=(0−4)2+(4−0)2=42
Khoảng cách từ O đến đường thẳng y=-x+4 là:
AH=OA⋅OBAB=164√2=2√2
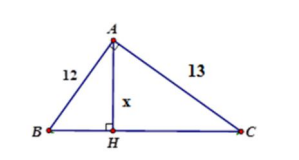
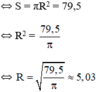



\(x=\sqrt{\dfrac{313}{24336}}\left(đvđd\right)\)
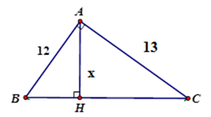
Áp dụng HTL ta có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
\(\Rightarrow\dfrac{313}{24336}=\dfrac{1}{x^2}\)
\(\Rightarrow x^2=1:\dfrac{313}{24336}\)
\(\Rightarrow x^2=\dfrac{24336}{313}\)
\(\Rightarrow x=\sqrt{\dfrac{24336}{313}}\approx8,82\)