K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
C
2
6 tháng 10 2021
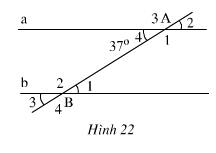
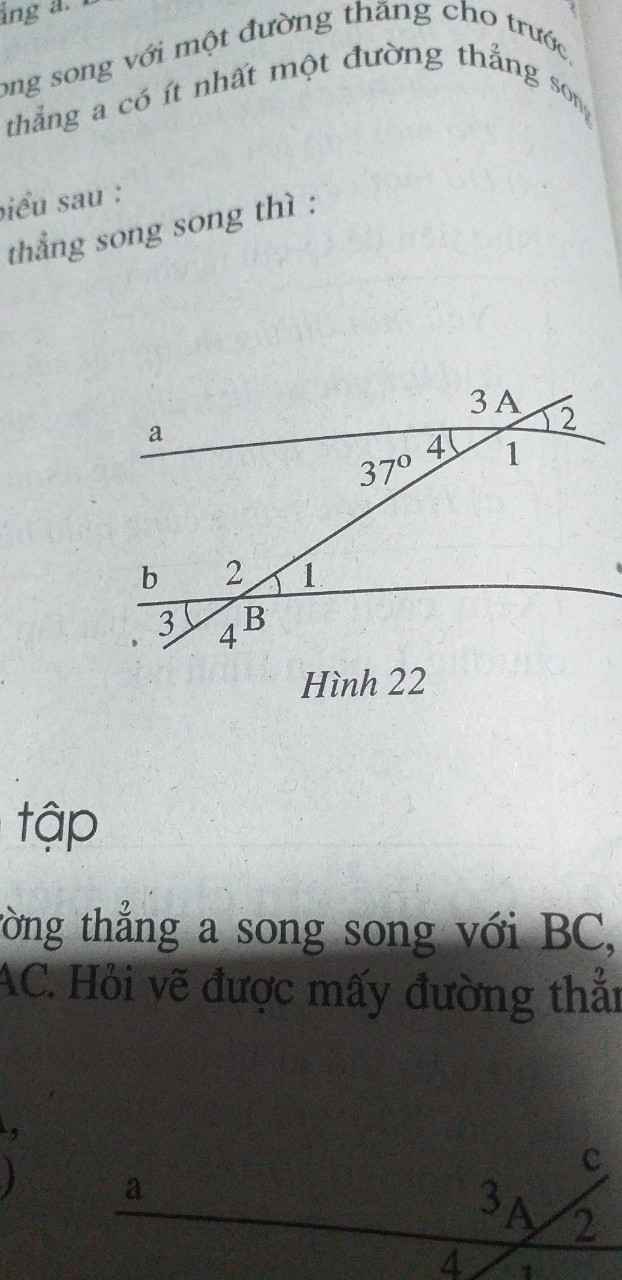
a, a//b \(\Rightarrow\widehat{A_4}=\widehat{B_1}=37^0\left(so.le.trong\right)\)
b, a//b \(\Rightarrow\widehat{A_1}=\widehat{B_4}\left(đồng.vị\right)\)
c, \(\widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{B_2}=180^0-37^0=143^0\)
11 tháng 12 2016
Ta có \(3^{22}=\left(3^2\right)^{11}=9^{11}\)
\(2^{33}=\left(2^3\right)^{11}=8^{11}\)
Ta có \(8< 9\Rightarrow8^{11}< 9^{11}\)
hay \(3^{22}>2^{33}\)
11 tháng 12 2016
Ta có 3^22= (3^2)^11=9^11(1)
2^33= (2^3)^11=8^11(2)
Từ (1) và (2) suy ra 3^22>2^33
Học tốt !
13 tháng 10 2021
mình nghĩ là 2^33 < 3^22
nấu sai thì bạn thông cảm nhé :)
NT
3
WJ
22 tháng 6 2016
a) \(3^{200}=\left(3^2\right)^{100}=9^{100}\) ; \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Vì 9> 8\(\Rightarrow9^{100}>8^{100}\)
Phần b mk chưa làm được
10 tháng 6 2017
\(\frac{-22}{35}\) và \(\frac{-103}{177}\)
\(=\frac{-22}{35}>\frac{-22}{177}>\frac{-103}{177}\)
\(\Rightarrow\frac{-22}{35}>\frac{-103}{177}\)
^^ Học tốt!
10 tháng 6 2017
(-22)/35 > -(103)/177
k và kb nha iu các bn nhìu
văn huân
BF
0
18 tháng 6 2015
3200 và 2300
3200=32.100=9100
2300=23.100=8100
Vì 9100 > 8100
Nên 3200 > 2300
912 và 268
912=93.4=7294
268=262.4=6764
Vì 7294 > 6764
Nên 912 > 268.
18 tháng 6 2015
Ta co :
\(3^{200}.va.2^{300}\)
\(3^{200}=\left(3^2\right)^{100}=\left(9\right)^{100}=9^{100}\) (1)
\(2^{300}=\left(2^3\right)^{100}=\left(8\right)^{100}\) (2)
Tu (1) va(2)
\(\Rightarrow9^{100}>8^{100}\)
Vay : \(3^{200}>2^{300}\)
Ta có: \(\left(2^2\right)^3=2^{2.3}=2^6\)
Vậy \(\left(2^2\right)^3=2^6\)
= nhau