Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(B=\frac{6}{8}+\frac{6}{56}+\frac{6}{140}+...+\frac{6}{1100}+\frac{6}{1400}\)
\(\Rightarrow B=\frac{3}{4}+\frac{3}{28}+\frac{3}{140}+...+\frac{3}{550}+\frac{3}{700}\)
\(\Rightarrow B=\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.10}+...+\frac{3}{22.25}+\frac{3}{25.28}\)
\(\Rightarrow B=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{22}-\frac{1}{25}+\frac{1}{25}-\frac{1}{28}\)
\(\Rightarrow B=1-\frac{1}{28}\)
\(\Rightarrow B=\frac{28}{28}-\frac{1}{28}=\frac{27}{28}\)
NHỚ TK MK NHA,MK ĐANG ÂM ĐIỂM
\(B=\frac{6}{8}+\frac{6}{56}+\frac{6}{140}+....+\frac{6}{1100}+\frac{6}{1400}\)
Rút gọn các phân số số ; ta được :
\(B=\frac{3}{4}+\frac{3}{56}+\frac{3}{70}+....+\frac{3}{550}+\frac{3}{700}\)
\(B=\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.10}+...+\frac{3}{22.25}+\frac{3}{25.28}\)
\(B=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{22}-\frac{1}{25}+\frac{1}{25}-\frac{1}{28}\)
\(B=1-\frac{1}{28}=\frac{27}{28}\)
Vậy biểu thức \(B=\frac{27}{28}\)

\(A=\dfrac{3}{4}+\dfrac{3}{28}+\dfrac{3}{140}+...+\dfrac{3}{550}+\dfrac{3}{700}\)
\(A=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{22.25}+\dfrac{3}{25.28}\)
\(A=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{22}-\dfrac{1}{25}+\dfrac{1}{25}-\dfrac{1}{28}\)
\(A=1-\dfrac{1}{28}\)
\(A=\dfrac{28}{28}-\dfrac{1}{28}=\dfrac{27}{28}\)

Lời giải:
Số số hạng của $A$: $\frac{102-5}{1}+1=98$
$A=\frac{(102+5).98}{2}=5243$
Số số hạng của $B$: $\frac{50-2}{3}+1=17$
$B=\frac{(50+2).17}{2}=442$
Số số hạng của $C$: $\frac{100-5}{5}+1=20$
$C=\frac{(100+5).20}{2}=1050$

a)\(\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+...+\frac{1}{195}\)
Đặt \(C=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{66}\)
\(\Rightarrow\frac{1}{2}C=\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{132}\)
\(\Rightarrow\frac{1}{2}C=\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{11.12}\)
\(\Rightarrow\frac{1}{2}C=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{11}-\frac{1}{12}\)
\(\Rightarrow\frac{1}{2}C=\frac{1}{4}+\left(-\frac{1}{5}+\frac{1}{5}\right)+\left(-\frac{1}{6}+\frac{1}{6}\right)+...+\left(-\frac{1}{11}+\frac{1}{11}\right)-\frac{1}{12}\)\(\Rightarrow\frac{1}{2}C=\frac{1}{4}+0+0+...+0-\frac{1}{12}\)
\(\Rightarrow\frac{1}{2}C=\frac{1}{4}-\frac{1}{12}\)
\(\Rightarrow\frac{1}{2}C=\frac{3}{12}-\frac{1}{12}\)
\(\Rightarrow\frac{1}{2}C=\frac{2}{12}\)
\(\Rightarrow\frac{1}{2}C=\frac{1}{6}\)
\(\Rightarrow C=\frac{1}{6}:\frac{1}{2}\)
\(\Rightarrow C=\frac{1}{6}\cdot2\)
\(\Rightarrow C=\frac{2}{6}=\frac{1}{3}\)


ta có: 1/1*6+1/6*11+1/6*16+...+1/51*56.
=1/5.(5/1.6+5/6.11+5/6.16+...+5/51.56)
=1/5.(1/1-1/6+1/6-...-1/56)
=1/5.(1-1/56)
=1/5.(55/56)
=11/56

Phân số thứ 3 you viết sai rồi
S6 = 10/56 + 10/140 + 10/260 + ... + 10/1400
2/10.S6 = 1/28 + 1/70 + 1/130 + ... + 1/700
6/10.S6 = 3/4.7 + 3/7.10 + 3/10.13 + ... + 3/25.28
3/5.S6 = 1/4 - 1/7 + 1/7 - 1/10 + 1/10 - 1/13 + ... + 1/25 - 1/28
3/5.S6 = 1/4 - 1/28
3/5.S6 = 7/28 - 1/28 = 3/14
Tự lm típ đc rồi nhé

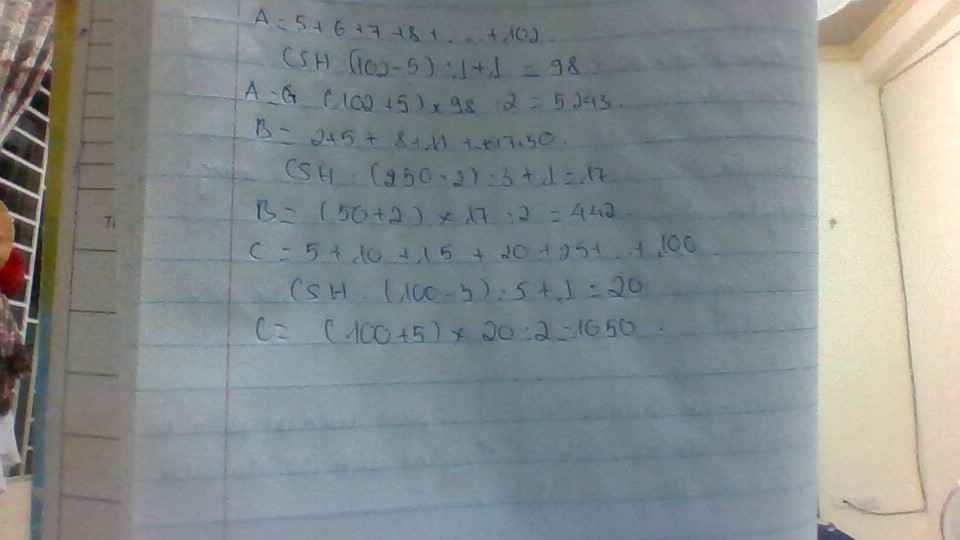
ta có A=\(\dfrac{6}{8}\)+\(\dfrac{6}{56}\)+\(\dfrac{6}{140}\)+...+\(\dfrac{6}{1100}\)+\(\dfrac{6}{1400}\)
=\(\dfrac{3}{4}\)+\(\dfrac{3}{28}\)+\(\dfrac{3}{70}\)+...+\(\dfrac{3}{550}\)+\(\dfrac{3}{700}\)
=\(\dfrac{3}{1.4}\)+\(\dfrac{3}{4.7}\)+\(\dfrac{3}{7.10}\)+...+\(\dfrac{3}{22.25}\)+\(\dfrac{3}{25.28}\)
=1-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{10}\)+...+\(\dfrac{1}{22}\)-\(\dfrac{1}{25}\)+\(\dfrac{1}{25}\)-\(\dfrac{1}{28}\)
=1-\(\dfrac{1}{28}\)
=\(\dfrac{27}{28}\)
Vậy A=\(\dfrac{27}{28}\)
Ta có:
A =6/8+6/56+6/140+...+6/1100+6/1400
⇒A=3/4+3/28+3/70+...+3/550+3/700
⇒A=3/1.4+3/4.7+3/7.10+...+3/22.25+3/25.28
⇒A=1−1/4+1/4−1/7+1/7−1/10+...+1/22−1/25+1/25−1/28
⇒A=1−1/28
⇒A=1-1/38