HT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
11 tháng 9 2019
Ta có
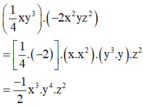
Đơn thức trên có hệ số bằng -1/2.
Bậc của tích trên là tổng bậc của các biến :
Biến x có bậc 3
Biến y có bậc 4
Biến z có bậc 2
⇒ Tích có bậc : 3 + 4 + 2 = 9.
28 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`-0,5x^2yz*(-3xy^3z)`
`= [(-0,5)*(-3)]*(x^2*x)*(y*y^3)*(z*z)`
`= 1,5x^3y^4z^2`
Hệ số: `1,5`
Bậc: `3+4+2 = 9`
`@` `\text {Kaizuu lv u}`
NT
1
26 tháng 3 2022
Câu 1 :
a, \(4x^4y^2.9x^2y^4z^2=36x^6y^6z^2\)
b, bậc 14 ; hệ số 36
biến x^6y^6z^2
PT
1
CM
27 tháng 2 2019
(-2x2yz).(-3xy3z) = [(-2).(-3)].(x2.x)(y.y3).(z.z) = 6.x3.y4.z2
Đơn thức trên có hệ số bằng 6.
Bậc của tích trên là tổng bậc của các biến :
Biến x có bậc 3
Biến y có bậc 4
Biến z có bậc 2
⇒ Tích có bậc : 3 + 4 + 2 = 9
ND
thu gọn đơn thức sau, rồi tìm bậc và hệ số của nó
(xy3)2.(-\(\dfrac{2}{5}\)x5).(\(\dfrac{5}{4}\)x2y8)
3
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2022
\(=-\dfrac{2}{5}.\dfrac{5}{4}.x^2.x^5.x^2.y^6.y^8=-\dfrac{1}{2}x^9y^{14}\)
Bậc của đa thức là: \(9+14=23\)
Hệ số là: \(-\dfrac{1}{2}\)
x2yz3). Thu gọn rồi tìm phần hệ số, phần biến và bậc của đơn thức A.
xy2.(x3y)(-3x13y5)0
6 tháng 3 2022
Bài 7
\(-3y\left(x^2y^2\right)\left(-x^3y^9\right)=3x^5y^{12}\)
hệ sô : 3 ; biến x^5y^12 ; bậc 17
