M
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CT
0
2 tháng 5 2017
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right).....\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right).....\left(1-\frac{2010}{2010}\right).\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right).....\left(1-1\right).\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right)\left(1-\frac{2}{2010}\right)\left(1-\frac{3}{2010}\right)....0.\left(1-\frac{2011}{2010}\right)\)
\(A=0\)
2 tháng 5 2017
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...\left(1-\frac{2010}{2010}\right).\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...0.\left(1-\frac{2011}{2010}\right)\)
\(\Rightarrow A=0\)
( Vì 0 nhân với số nào cũng bằng 0 )
KT
2
2 tháng 4 2015
A=\(\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right)...\left(1-\frac{2010}{2010}\right)\left(1-\frac{2011}{2010}\right)\)
A=\(\frac{2009}{2010}.\frac{2008}{2010}...0.\frac{-1}{2010}\)
A=0
LT
1
LT
1
26 tháng 6 2022
\(A=\dfrac{2009}{2010}\cdot\dfrac{2008}{2010}\cdot...\cdot\dfrac{2}{2010}\cdot\dfrac{1}{2010}\cdot\dfrac{0}{2010}\cdot\dfrac{-1}{2010}\)
=0
7 tháng 5 2017
\(B=\left(1-\frac{1}{2010}\right)x\left(1-\frac{2}{2010}\right)x\left(1-\frac{3}{2010}\right)x...x\left(1-\frac{2011}{2010}\right)\)
\(B=\left(1-\frac{1}{2010}\right)x\left(1-\frac{2}{2010}\right)x\left(1-\frac{3}{2010}\right)x....x\left(1-\frac{2010}{2010}\right)x\left(1-\frac{2011}{2010}\right)\)
\(B=\left(1-\frac{1}{2010}\right)x\left(1-\frac{2}{2010}\right)x\left(1-\frac{3}{2010}\right)x...x\left(0\right)x\left(1-\frac{2011}{2010}\right)\)
\(B=0\)
29 tháng 2 2016
trong dãy tích A sẽ có phân số \(1-\frac{2010}{2010}=1-1=0\)
=>A=0
DB
1
12 tháng 2 2018
(1 + 2 + 3 + 4 + ... + 2010).(1 + 22 + 33 + ... + 20102010 + 20112011).(170170 - 7.11.13.170)
= (1 + 2 + 3 + 4 + ... + 2010).(1 + 22 + 33 + ... + 20102010 + 20112011).(170170 - 170170)
= (1 + 2 + 3 + 4 + ... + 2010).(1 + 22 + 33 + ... + 20102010 + 20112011). 0
= 0
27 tháng 4 2016
\(A=\frac{ }{ }sdadsad\text{đ}\text{s}gh\text{d}fg\text{d}\)sf
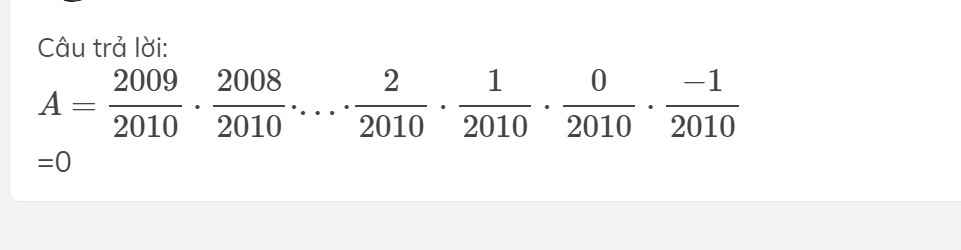
Ta có:\(1-\frac{2010}{2010}=1-1=0\)
Tích A= (1-1/2010).(1-2/2010).(1-3/2010)....(1-2011/2010) chứa thừa số \(1-\frac{2010}{2010}=0\)
Vậy tích A=(1-1/2010).(1-2/2010).(1-3/2010)....(1-2011/2010)=0(Vì có chứa thừa số 0)
Ta có \(1-\frac{2010}{2010}=1-1=0\)
Mà \(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...\left(1-\frac{2010}{2010}\right).\left(1-\frac{2011}{2010}\right)\)
Nên \(A=...0\)\(=0\)