Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{n\left(n+1\right)}=\frac{2013}{2014}\)
\(\Rightarrow1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}=\frac{2013}{2014}\)
\(\Rightarrow1-\frac{1}{n+1}=\frac{2013}{2014}\)
\(\Rightarrow\frac{1}{n+1}=1-\frac{2013}{2014}\)
\(\Rightarrow\frac{1}{n+1}=\frac{1}{2014}\)
\(\Rightarrow n+1=2014\)
\(\Rightarrow n=2014-1\)
\(\Rightarrow n=2013\)

\(\dfrac{3x^4-2x^3+7x-1}{x^2-x+1}\)
\(=\dfrac{3x^4-3x^3+3x^2+x^3-x^2+x-2x^2+2x-2+4x+1}{x^2-x+1}\)
\(=3x^2+x-2+\dfrac{4x+1}{x^2-x+1}\)

a: \(5x^2\left(3x^3-2x^2+x+2\right)\)
\(=15x^5-10x^4+5x^3+10x^2\)
b: \(3x^4\left(-2x^3+5x^2-\dfrac{2}{3}x+\dfrac{1}{3}\right)\)
\(=-6x^7+15x^6-2x^5+x^4\)


\(\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+5\right)\)
\(=x^2+x+2x+2-x^2-5x+3x+15\)
\(=x+15\)

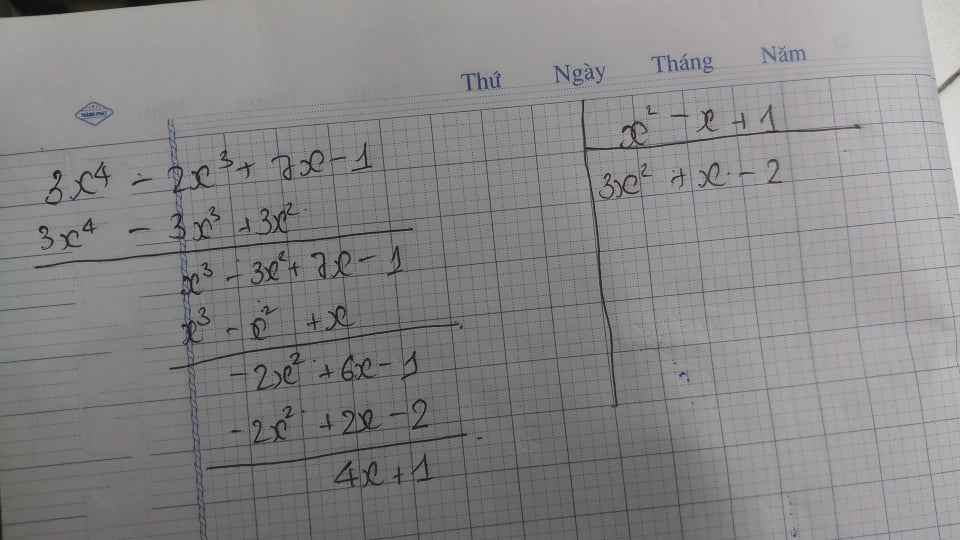
program tinhtoan;
uses crt;
var: i;n:interger;
S:real;
writeln(' Nhap n='); readln(n);
S:=0;
For i:=1 to n*(n*1) do S:=S+\(\frac{1}{i};\)
writeln(' S=',S);
End.
(ps: ko chắc )