Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

dịch
Các bạn giúp mìn bài nì ha. Bạn nào giải được trong vòng 5 phút thì mìn thanks lém lém:
Tính A= 1.3^3+3.5^3+5.7^3+...+n.(n+2)^3(với n là số tự nhiên lẻ)

A bn lướt xuống dưới mà xem cách làm
nhưng của bn là cho 3 ra ngoài nha![]()

ta có 2/n(n+2)=1/n-1/(n+2)
nên 2/3.5=1/3-1/5
2^2/3.5+2^2/5.7+2^2/7.9+...+2^2/49.51
=2.{2/3.5+2/5.7+..+2/49.51}
=2{1/3-1/5+1/5-1/7+...+1/49-1/51}
=2{1/3-1/51}=32/51

\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2020}\)\(-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}\)
\(=\dfrac{2021}{2022}\)

Vì 2 tia Ox và Oy đối nhau \(\Rightarrow\)\(\widehat{xOy}=180^0\)
Vì \(\widehat{xOy}=180^0\)nên Oz nằm giữa Ox và Oy
\(\Rightarrow\widehat{xOy}=\widehat{xOz}+\widehat{yOz}=180^0\)
Theo bài ra ta có: \(\widehat{xOz}+40^0=\widehat{yOz}\)
\(\Rightarrow\widehat{yOz}-\widehat{xOz}=40^0\)
\(\Rightarrow\widehat{xOz}=\left(180^0-40^0\right)\div2=70^0\)
\(\widehat{yOz}=70^0+40^0=110^0\)

\(A=\frac{3}{2\cdot4}+\frac{3}{4\cdot6}+...+\frac{3}{48\cdot50}\)---> Mik nghĩ bn ghi nhầm :]
\(A=\frac{3}{2}\left[\frac{1}{2\cdot4}+\frac{1}{4\cdot6}+...+\frac{1}{48\cdot50}\right]\)
\(A=\frac{3}{2}\left[\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+...+\frac{1}{48}-\frac{1}{50}\right]\)
\(A=\frac{3}{2}\left[\frac{1}{2}-\frac{1}{50}\right]=\frac{3}{2}\cdot\frac{12}{25}=\frac{18}{25}\)
Vậy A = 18/25
\(B=\frac{5}{1\cdot3}+\frac{5}{3\cdot5}+...+\frac{5}{49\cdot51}\)
\(B=\frac{5}{2}\left[\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+...+\frac{1}{49\cdot51}\right]\)
\(B=\frac{5}{2}\left[\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{49}-\frac{1}{51}\right]\)
\(B=\frac{5}{2}\left[1-\frac{1}{51}\right]=\frac{5}{2}\cdot\frac{50}{51}=\frac{125}{51}\)

a) pt => 2x-x=-25+5(chuyển vế đổi dấu) =>x=-20
b)pt=>\(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{2x-1}-\frac{1}{2x+1}\)=\(\frac{2016}{2017}\)
=>\(1-\frac{1}{2x+1}=\frac{2016}{2017}\)=>\(\frac{2x}{2x+1}=\frac{2016}{2017}\). Nhân chéo => x=1008
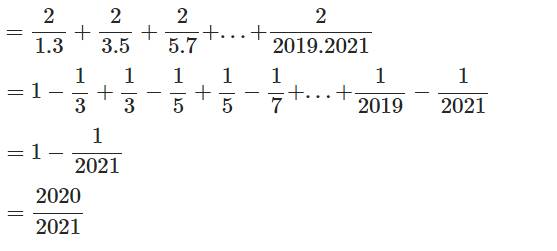
\(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{49.51}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{49}-\frac{1}{51}\)
\(=1-\frac{1}{51}=\frac{50}{51}\)
2/1.3 + 2/3.5 + 2/5.7 + ... + 2/49 . 51
= 2/1.3 + 2/3.5 + 2/5.7 + ... + 2/49 . 51
= 1 + 51 = 52