Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{99^2}+\dfrac{1}{100^2}\)
\(< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\)
\(B=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\) \(\Rightarrow A< \dfrac{99}{100}\)
\(1-\dfrac{1}{2^2}-\dfrac{1}{3^2}-...-\dfrac{1}{100^2}=1-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}\right)=1-A>\dfrac{1}{100}\)

\(B=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\dfrac{1}{64}\)
=>\(B=\dfrac{32}{64}+\dfrac{16}{64}+\dfrac{6}{64}+\dfrac{2}{64}+\dfrac{1}{64}\)
=>\(B=\dfrac{32+16+6+2+1}{64}\)
=>\(B=\dfrac{63}{64}\)

Lời giải:
Xét tử số:
$X=1+2+2^2+2^3+...+2^{2008}$
$2X=2+2^2+2^3+2^4+....+2^{2009}$
$\Rightarrow 2X-X=(2+2^2+2^3+2^4+....+2^{2009})-(1+2+2^2+...+2^{2008})$
$\Rightarrow X=2^{2009}-1$
$\Rightarrow S=\frac{X}{1-2^{2009}}=\frac{2^{2009}-1}{-(2^{2009}-1)}=-1$

Lời giải:
$S=\frac{1}{7^2}+\frac{2}{7^3}+\frac{3}{7^4}+...+\frac{69}{7^{70}}$
$7S=\frac{1}{7}+\frac{2}{7^2}+\frac{3}{7^3}+...+\frac{69}{7^{69}}$
$6S=7S-S=\frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+....+\frac{1}{7^{69}}-\frac{69}{7^{70}}$
$42S=1+\frac{1}{7}+\frac{1}{7^2}+...+\frac{1}{7^{68}}-\frac{69}{7^{69}}$
$\Rightarrow 42S-6S=(1+\frac{1}{7}+\frac{1}{7^2}+...+\frac{1}{7^{68}}-\frac{69}{7^{69}})-(\frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+....+\frac{1}{7^{69}}-\frac{69}{7^{70}})$
$\Rightarrow 36S=1-\frac{69}{7^{69}}-\frac{1}{7^{69}}+\frac{69}{7^{70}}$
Hay $36S=1-\frac{69.7-7-69}{7^{70}}=1-\frac{407}{7^{70}}$
$\Rightarrow S=\frac{1}{36}(1-\frac{407}{7^{70}})$
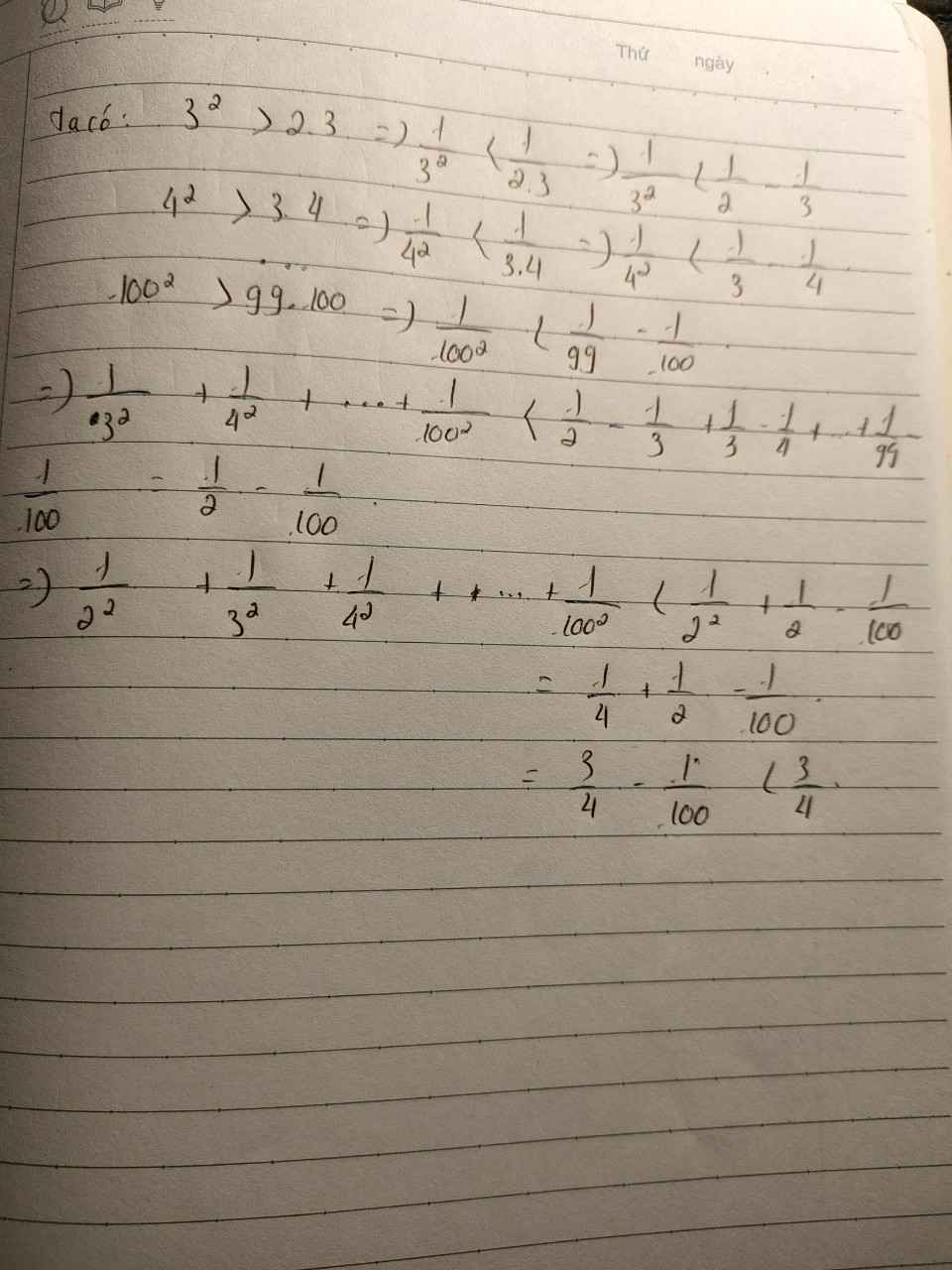
N=1/2+1/22+...+1/210
2N=1+1/2+...+1/29
2N-N=1-1/210=1-1/1024=1023/1024
Giải:
N=1/2+1/22+1/23+...+1/29+1/210
2N=1+1/2+1/22+...+1/28+1/29
2N-N=(1+1/2+1/22+...+1/28+1/29)-(1/2+1/22+1/23+...+1/29+1/210)
N=1-1/210=1023/1024
Chúc bạn học tốt!