Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Hợp lực của F1 và F2 là:
F12 = 2.F1.cosα/2 = 2.20.cos30o
![]()
F3 vuông góc với mp chứa F1 và F2 nên F3 vuông góc với F12.
Hợp lực của ba lực chính là hợp lực của F12 và F3.
Ta có:
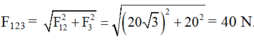
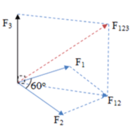

Đáp án D
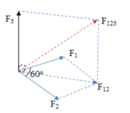
Hợp lực của F1 và F2 là:
F 12 = 2. F 1 . cos α 2 = 2.20. cos 30 0 = 20 3 N
F3 vuông góc với mp chứa F1 và F2 nên F3 vuông góc với F12.
Hợp lực của ba lực chính là hợp lực của F12 và F3.
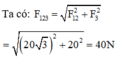

Tóm tắt: \(F_1=F_2=20N\)\(;F_{hl}=20N\)
\(\alpha=?\)
Bài giải:
Gọi góc giữa hai lực này là \(\alpha\)
Ta có: \(F^2=F_1^2+F_2^2+2F_1\cdot F_2\cdot cos\alpha\)
\(\Rightarrow cos\alpha=\dfrac{F^2-F_1^2-F_2^2}{2\cdot F_1\cdot F_2}=\dfrac{20^2-20^2-20^2}{2\cdot20\cdot20}=-\dfrac{1}{2}\)
\(\Rightarrow\alpha=120^o\)
Chọn D.

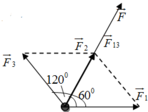
Theo bài ra ( F 1 → ; F → 3 ) = 120 0 ; F 1 = F 3 nên theo quy tắc tổng hợp hình bình hành và tính chất hình thoi ta có
( F 1 → ; F → 13 ) = 60 0 ; F 1 = F 3 = F 13 = 60 N
Mà ( F 1 → ; F → 2 ) = 60 0 ⇒ F → 2 ↑ ↑ F → 13
Vậy F = F 13 + F 2 = 60 + 60 = 120

Chọn B.
Ta tổng hợp theo phương pháp số phức:
+ Chọn trục trùng véc tơ F 1 → làm trục chuẩn thì F 2 → sớm hơn F 1 → một góc 600 và F 3 → sớm hơn F 1 → một góc 1200.
+ Tổng phức:
![]()
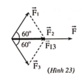
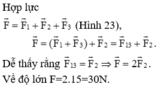
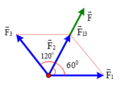
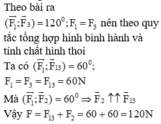

Gọi F 2 → là lực có góc hợp với hai lực còn lại đều là các góc 60 ∘
Vẽ hình, ta có:
+ Tổng hợp lực: F 12
Ta có:
F 12 = F 1 2 + F 2 2 + 2 F 1 F 2 cos 60 0 = 20 2 + 20 2 + 2.20.20. c os 60 0 = 20 3 N
Lại có góc hợp bởi F 12 → , F 2 → = 30 0
Ta suy ra, góc hợp bởi F 12 → , F 3 → = 30 0 + 60 0 = 90 0
+ Hợp lực của ba lực: F = F 12 2 + F 3 2 = 20 3 2 + 20 2 = 40 N
Đáp án: B