Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Việc gọi ẩn ko ảnh hưởng gì tới kết quả bài toán cả, cứ thoải mái đi

Cứ áp dụng công thức \(\left(ln\left|u\right|\right)'=\dfrac{u'}{u}\) thôi
Còn câu dưới thì: \(\int\dfrac{axdx}{x^2\sqrt{x^2+a}}\)
Đặt \(u=\sqrt{x^2+a}\Rightarrow x^2=u^2-a\Rightarrow xdx=udu\)
\(\Rightarrow I=\int\dfrac{a.u}{u\left(u^2-a\right)}du\)
Nguyên hàm hữu tỉ khá cơ bản, tách ra bằng hệ số bất định
CMR \(F\left(x\right)=ln\dfrac{x^2-x\sqrt{2} 1}{x^2 x\sqrt{2} 1}\) là 1 nguyên hàm của hàm số \(f\left(x\right)=\dfrac{2... - Hoc24
Hi câu này nữa anh :>

Họ đã check kĩ câu trả lời rồi ms nhé ! còn mấy bn chỉ lm mấy bài dễ lm sao đc ?

\(V=\dfrac{1}{3}SA.S_{ABCD}\Rightarrow S_{ABCD}=\dfrac{3V}{SA}=22\sqrt{3}\)
\(\Rightarrow\dfrac{1}{2}AB.AD+\dfrac{1}{2}BC.CD=22\sqrt{3}\)
\(\Leftrightarrow5AD+3CD=44\) (1)
Mặt khác: \(\left\{{}\begin{matrix}BD^2=AB^2+AD^2=AD^2+75\\BD^2=BC^2+CD^2=CD^2+27\end{matrix}\right.\)
\(\Rightarrow AD^2+75=CD^2+27\Rightarrow AD^2+48=CD^2\) (2)
Giải hệ (1) và (2) ta được \(\left\{{}\begin{matrix}AD=4\\CD=8\end{matrix}\right.\)
Từ A kẻ \(AH\perp BD\) \(\Rightarrow BD\perp\left(SAH\right)\) \(\Rightarrow\left(SBD\right)\) và (ABCD) đều vuông góc (SAH)
\(\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và đáy
Hệ thức lượng tam giác vuông ABD:
\(\dfrac{1}{AH^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{91}{1200}\Rightarrow AH=\dfrac{20\sqrt{273}}{91}\)
\(cot\widehat{SHA}=\dfrac{AH}{SA}=\dfrac{20\sqrt{273}}{819}\)
gọi x là độ dài cạnh AD; y là độ dài cạnh CD
\(\Rightarrow S_{ABCD}=S_{BAD}+S_{BCD}=\dfrac{1}{2}.AB.AD+\dfrac{1}{2}BC.CD=\dfrac{1}{2}5\sqrt{3}x+\dfrac{1}{2}3\sqrt{3}y\)
\(\Rightarrow V_{SABCD}=\dfrac{1}{3}SA.S_{ABCD}=\dfrac{1}{3}.9.\left(\dfrac{1}{2}.5\sqrt[]{3}x+\dfrac{1}{2}3\sqrt{3}y\right)=\dfrac{3\sqrt{3}}{2}\left(5x+3y\right)=66\sqrt{3}\\ \Rightarrow5x+3y=44\)
\(AH\perp BD\left(H\in BD\right)\\ cot\left(\left(SBD\right),\left(ABCD\right)\right)=\widehat{SHA}\Rightarrow cot\widehat{SHA}=\dfrac{SA}{AH}\)
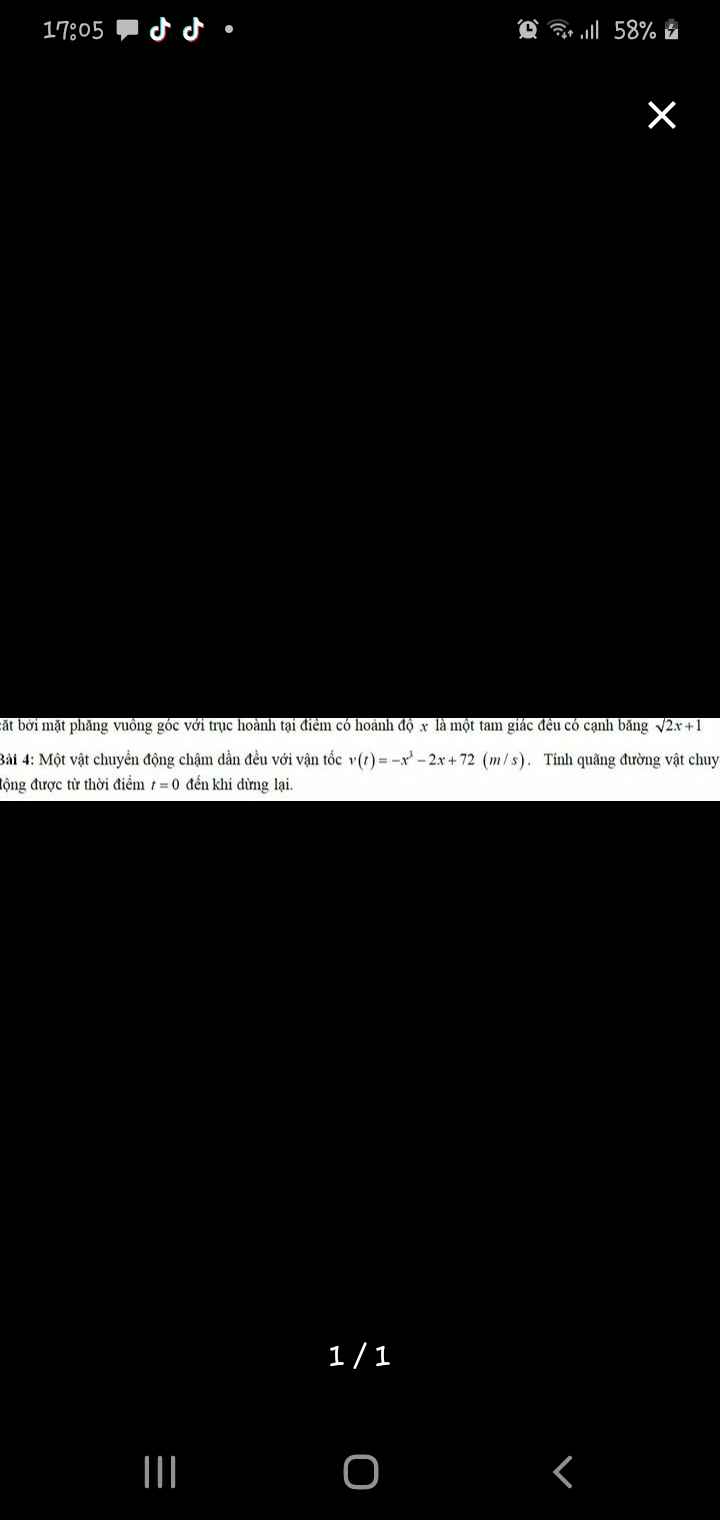 Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
Số âm k đc ở trg căn nhé
Sai bạn nhé! Cấp 3 có học tập hợp số phức (hay số ảo) nghĩa là trong đó có số i sao cho i2=-1. Nên kq là :
= -3i + (-2i)
=-5i