Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn ơi câu a t chưa làm chưa biết nhưng câu b chắc chắn có Max tại x=-3 nhé ! Nếu bn chỉ tìm ra Min là chưa đủ

Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$

Đặt \(t=\sin^2x\Rightarrow\begin{cases}\cos^2x=1-t\\t\in\left[0;1\right]\end{cases}\) \(\Leftrightarrow f\left(x\right)=5^t+5^{1-t}=g\left(t\right);t\in\left[0;1\right]\)
Ta có : \(g'\left(t\right)=5^t\ln5-5^{1-t}\ln5=\left(5^t-5^{1-t}\right)\ln5=0\)
\(\Leftrightarrow5^t=5^{1-t}\)
\(\Leftrightarrow t=1-t\)
\(t=\frac{1}{2}\)
Mà \(\lim\limits_{x\rightarrow-\infty}g\left(t\right)=\lim\limits_{x\rightarrow-\infty}\left(5^t-5^{1-t}\right)=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}g\left(t\right)=\lim\limits_{x\rightarrow+\infty}\left(5^t-5^{1-t}\right)=+\infty\)
Ta có bảng biến thiên
\(\Rightarrow\) Min \(f\left(x\right)=2\sqrt{5}\) khi \(t=\frac{1}{2}\Leftrightarrow\sin^2x=\frac{1}{2}\Leftrightarrow\frac{1-\cos2x}{2}=\frac{1}{2}\)
\(\Leftrightarrow\cos2x=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\) \(\left(k\in Z\right)\)

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

\(f'\left(x\right)=2-\dfrac{\pi}{2}sin\left(\dfrac{\pi x}{3}\right)=\dfrac{1}{2}\left(4-\pi sin\left(\dfrac{\pi x}{2}\right)\right)\)
Do \(\left|\pi sin\left(\dfrac{\pi x}{2}\right)\right|\le\pi< 4\Rightarrow f'\left(x\right)>0\) ; \(\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow f\left(x\right)_{min}+f\left(x\right)_{max}=f\left(-2\right)+f\left(2\right)=-4+cos\left(-\pi\right)+4+cos\left(\pi\right)=-2\)

Chọn B
Vì y = a x 3 + c x + d , a ≠ 0 là hàm số bậc ba và có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) nên a < 0 và y' = 0 có hai nghiệm phân biệt.
Ta có ![]() có hai nghiệm phân biệt
⇔
ac < 0
có hai nghiệm phân biệt
⇔
ac < 0
Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau 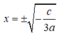
Từ đó suy ra
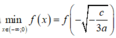
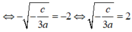
⇔
c = -12a
Ta có bảng biến thiên
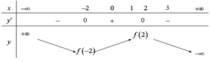
Ta suy ra ![]()

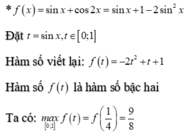


Đáp án C
Áp dụng bất đẳng thức Bunhiacopxki ta có
Suy ra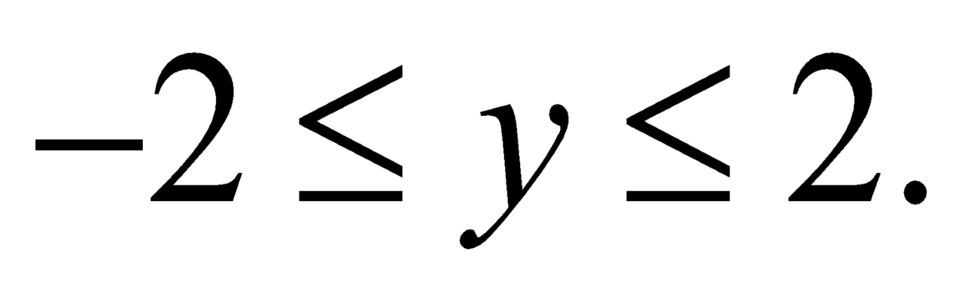 Giá trị y = 2 đặt được khi
Giá trị y = 2 đặt được khi 