Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(M=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m+n\right)^2\left(m-n\right)\)
\(=\left(-2017+2017\right)^2\cdot\left(-2017-2017\right)\)
=0
b: \(N=n^3-3n^2-n\left(3-n\right)\)
\(=n^2\left(n-3\right)+n\left(n-3\right)\)
\(=n\left(n-3\right)\left(n+1\right)\)
\(=13\cdot10\cdot14=1820\)

Bài 1:
e: Ta có: \(x\left(y-x\right)^2-x^2+2xy-y^2\)
\(=x\left(x-y\right)^2-\left(x-y\right)^2\)
\(=\left(x-y\right)^2\cdot\left(x-1\right)\)
Bài 2:
a: Ta có: \(M=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m+n\right)^2\cdot\left(m-n\right)\)
\(=\left(-2017+2017\right)^2\cdot\left(-2017-2017\right)\)
=0

\(A=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m^2-n^2\right)\left(m+n\right)\)
Thay \(m=-2017;n=2017\) vào A , ta được :
\(A=\left[\left(-2017\right)^2-2017^2\right]\left(-2017+2017\right)=0\)
Vậy \(A=0\) tại \(m=-2017;n=2017\)
\(B=x^3-3x^2-x\left(3-x\right)\)
\(=x^2\left(x-3\right)+x\left(x-3\right)\)
\(=\left(x^2+x\right)\left(x-3\right)\)
\(=x\left(x+1\right)\left(x-3\right)\)
Thay \(x=13\) vào B , ta được :
\(13\left(13+1\right)\left(13-3\right)=13.14.10=1820\)
Vậy \(B=1820\) tại \(x=13\)

b: \(N=a^3-3a^2-a\left(3-a\right)\)
\(=a^2\left(a-3\right)+a\left(a-3\right)\)
\(=a\left(a-3\right)\left(a+1\right)\)

a) M = ( 2 m + 1 ) 3 khi m = 24,5 thì M = 50 3 = 125000.
b) N = n 3 − 1 3 khi n = 303 thì M = 100 3 .
c) Q = m n + 1 − 5 3 = m n − 4 3 khi m = 12; n = 2 thì Q = 2 3 = 8.

\(B=m^2-mn+m-n^2-n+mn=m^2-n^2+n-n\\ =\left(m-n\right)\left(m+n+1\right)\\ =\left(-\dfrac{2}{3}+\dfrac{1}{3}\right)\left(-\dfrac{2}{3}-\dfrac{1}{3}+1\right)=-\dfrac{1}{3}\cdot0=0\)
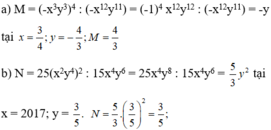
a) M = 0. b) N = 1820.