Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: B=|x-2|+|6-x|+5>=|x-2+6-x|+5=9
Dấu = xảy ra khi 2<=x<=6
4: B=|4-2x|+|2x+5|>=|4-2x+2x+5|=9
Dấu = xảy ra khi -5/2<=x<=2

Bài 2:
a) \(A=x^2+6\ge6>0\forall x\in R\)
b) \(B=\left(5-x\right)\left(x+8\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}5-x>0\\x+8>0\end{matrix}\right.\\\left\{{}\begin{matrix}5-x< 0\\x+8< 0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}5>x\ge-8\left(nhận\right)\\-8>x>5\left(VLý\right)\end{matrix}\right.\)

$A=(x-4)^2+1$
Ta thấy $(x-4)^2\geq 0$ với mọi $x$
$\Rightarroe A=(x-4)^2+1\geq 0+1=1$
Vậy GTNN của $A$ là $1$. Giá trị này đạt tại $x-4=0\Leftrightarrow x=4$
-------------------
$B=|3x-2|-5$
Vì $|3x-2|\geq 0$ với mọi $x$
$\Rightarrow B=|3x-2|-5\geq 0-5=-5$
Vậy $B_{\min}=-5$. Giá trị này đạt tại $3x-2=0\Leftrightarrow x=\frac{2}{3}$
$C=5-(2x-1)^4$
Vì $(2x-1)^4\geq 0$ với mọi $x$
$\Rightarrow C=5-(2x-1)^4\leq 5-0=5$
Vậy $C_{\max}=5$. Giá trị này đạt tại $2x-1=0\Leftrightarrow x=\frac{1}{2}$
----------------
$D=-3(x-3)^2-(y-1)^2-2021$
Vì $(x-3)^2\geq 0, (y-1)^2\geq 0$ với mọi $x,y$
$\Rightarrow D=-3(x-3)^2-(y-1)^2-2021\leq -3.0-0-2021=-2021$
Vậy $D_{\max}=-2021$. Giá trị này đạt tại $x-3=y-1=0$
$\Leftrightarrow x=3; y=1$
Ta có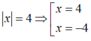
+ Trường hợp 1: x = 4 : Thay x = 4 vào biểu thức ta có:
5 . 4 2 - 2 . 4 - 18 = 5 . 16 - 8 - 18 = 80 - 8 - 18 = 54
Vậy B = 54 tại x = 4
+ Trường hợp 2: x = -4 : Thay x = -4 vào biểu thức ta có:
5 . - 4 2 - 2 . ( - 4 ) - 18 = 5 . 16 + 8 - 18 = 80 + 8 - 18 = 70
Vậy B = 70 tại x = -4
Với |x| = 4 thì B = 54 hoặc B = 70
Chọn đáp án C