

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hình chóp tứ giác đều cạnh đáy bằng 6cm, chiều cao hình chóp bằng 5cm.
Tương tự hình vẽ câu a ta có MA Δ BC.
Vì AO là đường cao của hình chóp nên △ AOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 25 + 9 = 34
Suy ra: AM = 34 cm
Ta có: S x q =6.2. 34 =12 34 ( c m 2 )
S đ á y = 6.6 = 36 ( c m 2 )
Vậy S T P = S x q + S đ á y = 12 34 +36 ≈ 106 ( c m 2 )

Hình chóp tứ giác đều, cạnh đáy bằng 20cm, chiều cao hình chóp bằng 7cm
Tương tự hình vẽ câu a ta có MA Δ BC
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
A M 2 = O A 2 + O M 2 = 49 + 100 = 149
Suy ra: AM = 149 cm
Ta có: S x q =20.2. 149 =40 149 ( c m 2 )
S đ á y = 20.20= 400( c m 2 )
Vậy S T P = S x q + S đ á y = 40 149 +400 ≈ 888,3( c m 2 )

Hình chóp tứ giác đều, cạnh đáy bằng 1m, chiếu cao hình chóp bằng 0,5m.
Tương tự hình vẽ câu a ta có AM Δ BC.
Vì AO là đường cao của hình chóp nên ΔAOM vuông tại O.
Áp dụng định li Pi-ta-go vào tam giác vuông AOM,ta có:
A M 2 = O A 2 + O M 2 = 0 , 5 2 + 0 , 5 2 = 0 , 5
Suy ra: AM = 0,5 cm
Ta có: S x q =1.2. 0 , 5 =2 0 , 5 ( m 2 )
S đ á y = 1.1=1( m 2 )
Vậy S T P = S x q + S đ á y = 2 0 , 5 + 1 ≈ 2,4( m 2 )

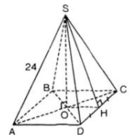
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 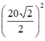 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
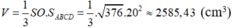
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 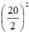 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).