Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Phương pháp
Sử dụng công thức tính diện tích mặt phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox và hai đường thẳng x=a,x=b là
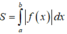
Chú ý đến dấu của f(x) khi phá dấu giá trị tuyệt đối. Nếu đồ thị nằm dưới Ox thì f(x)<0, nếu đồ thị nằm trên Ox thì f(x)>0.
Cách giải
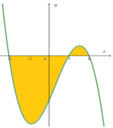
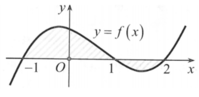
Trên (-2;1) thì đồ thị nằm phía dưới Ox nên f(x)<0, trên khoảng (1;2) thì đồ thị nằm trên Ox nên f(x)>0
Nên từ hình vẽ ta có diện tích phần được tô đậm là
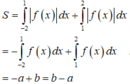

Đáp án B
Dựa vào hình vẽ ta có S = ∫ − 1 1 f x d x − ∫ 1 2 f x d x

Đáp án D
Giả sử đồ thị hàm số có dạng y = ax 3 + b x 2 + c x + d
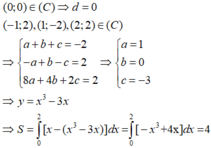

D
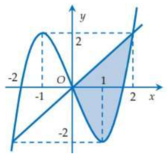
Từ đồ thị của hàm số đối xứng qua trục tung nên đáp án A và B đúng.
Do ∫ 0 2 f x d x = ∫ 0 1 f x d x + − ∫ 1 2 f x d x
= ∫ 0 1 f x d x + − ∫ 1 2 f x d x
Nên đáp án C đúng. Vậy chọn đáp án D

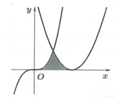
Hoành độ giao điểm của (C) và (P) là nghiệm phương trình: ![]()
Hoành độ giao điểm của (P) và Ox là nghiệm phương trình:
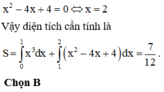
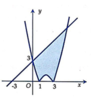
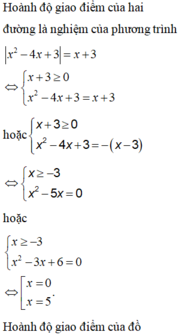
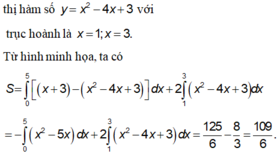


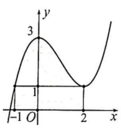
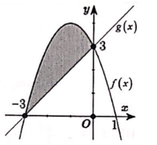
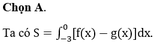
Đáp án A
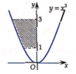
Cách 1: Xét phương trình:
x 2 = 3 ⇔ x = ± 3 ; x 2 = 1 ⇔ x = 1
Quan sát hình vẽ:
Diện tích hình phẳng giới hạn bởi các đường y = x 2 , y = 3, x = 0 là
S 1 = ∫ − 3 0 x 2 − 3 d x = ∫ − 3 0 x 2 − 3 d x = x 3 3 − 3 x 0 − 3 = 2 3
(đvdt).
Diện tích hình phẳng giới hạn bởi các đường y = x 2 , y = 1, x = 0 là
S 2 = ∫ − 1 0 x 2 − 1 d x = ∫ − 1 0 x 2 − 1 d x = x 3 3 − x 0 − 1 = 2 3
(đvdt).
Vậy diện tích hình phẳng cần tính là S = S 1 − S 2 = 2 3 − 2 3 (đvdt).
Cách 2: Ta có y = x 3 ⇔ y ≥ 0 x = ± y . Từ hình vẽ ta thấy x < 0 ⇒ x = − y .
Diện tích hình phẳng cần tính là:
S = ∫ 1 3 − y − 0 d y = ∫ 1 3 y d y = 2 y 3 3 3 1 = 2 3 − 2 3
(đvdt).