Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có hình vẽ :
Dễ thấy SABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)
mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)
=> SABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)
Khi 2 đường chéo vuông góc với nhau thì
\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)
hay \(sin\alpha=1\)
Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm)

Qua 4 đỉnh A,B,C,D của tứ giác ABCD đã cho, dựng các đường thẳng song song với 2 đường chéo AC,BD. Chúng cắt nhau tại 4 điểm M,N,P,Q. Khi đó ta có tứ giác MNPQ,AOBM,AODN,DOCP,BOCQ là các hình bình hành.
Suy ra MQ = NP = AC = 5,3 (cm), MN = PQ = BD = 4 (cm)
Đồng thời ^MNP = ^MQP = ^AOD = 700 (Các góc có 2 cạnh tương ứng song song)
Ta cũng có SAOD = SAND = SAODN/2. Từ đó SABCD = SMNPQ/2 = SMQP = SMNP
Xét \(\Delta\)MNP: MN = 4, NP = 5,3, ^MNP = 700
Có SMNP = 1/2.MN.NP.Sin^MNP = 4.5,3.Sin700 \(\approx\)19,9 (cm2) => SABCD\(\approx\)19.9 (cm2)
Kết luận: ...

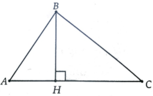
a, Giả sử tam giác ABC có A ^ < 90 0 kẻ đường cáo BH. Ta có BH=AB.sin A ^
=> S ∆ A B C = 1 2 A C . B H = 1 2 A B . A C . sin A
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có
A
O
B
^
=
α
<
90
0
. Kẻ AH
⊥
BD, tại H và CK
⊥
BD tại K
Ta có: AH = OA.sinα
=> S A B D = 1 2 B D . A H = 1 2 B D . O A . sin α
Tương tự: S C B D = 1 2 B D . C K = 1 2 B D . O C . sin α
=> S A B C D = S A B D + S C B D = 1 2 B D . O A . sin α + 1 2 B D . O C . sin α = 1 2 B D . A C . sin α
