K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
.
PT
1
PT
1
CM
1 tháng 1 2019
Đặt f(x) = 2x3 – 6x + 1
TXĐ: D = R
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0
f(0) = 1 > 0
f(1) = 2.13 – 6.1 + 1 = -3 < 0.
⇒ f(-2).f(0) < 0 và f(0).f(1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)
⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.
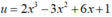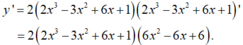
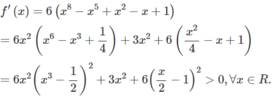
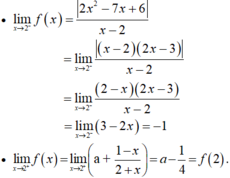
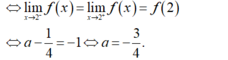
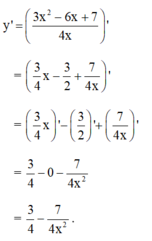
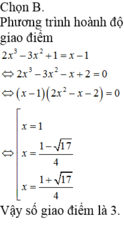
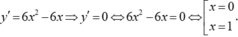
Chọn D.
Sử dụng công thức đạo hàm của hàm hợp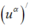
với u = 2x3 – 6x + 1
y' = 2(2x3 – 3x2 + 6x + 1)(2x3 – 3x2 + 6x + 1)’ = 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6).