NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 8 2018
x7-26x6+27x5-47x4-77x3+50x2+x-24
=x7-25x6-x6+25x5+2x5-50x4+3x4-75x3-2x3+50x2+x-24
= x6(x+(-25))-x5(x-25)+2x4(x-25)+3x3(x-25)
-2x2(x-25)+x-24
Thay x=25 vào biểu thức :
=>25 -24=1
Vậy C=1
HN
4
29 tháng 7 2020
Giá trị của biểu thức C tại x=25 là C(25).
Theo định lý Bezout, C(25) = số dư khi chia C(x) cho x-25.
Ta dùng sơ đồ Hooc-ne để tìm số dư này:
| 1 | -26 | 27 | -47 | -77 | 50 | 1 | -24 | |
| x=25 | 1 | -1 | 2 | 3 | -2 | 0 | 1 | 1 |
Vậy: C(25)=1 (Bạn có thể dùng máy tính kiểm tra).
PT
1
13 tháng 11 2021
\(1,\Leftrightarrow x^2+10x+25=x^2-4x-21\\ \Leftrightarrow14x=-46\\ \Leftrightarrow x=-\dfrac{23}{7}\\ 2,\Leftrightarrow x^3+8=15+x^3+2x\\ \Leftrightarrow2x=-7\Leftrightarrow x=-\dfrac{7}{2}\\ 3,\Leftrightarrow\left(x+3\right)^2=0\\ \Leftrightarrow x=-3\\ 4,\Leftrightarrow x^3-9x^2+27x-27=0\\ \Leftrightarrow\left(x-3\right)^3=0\\ \Leftrightarrow x-3=0\Leftrightarrow x=3\\ 5,\Leftrightarrow4x^2+4x+1-4x^2-16x-16=9\\ \Leftrightarrow-12x=24\Leftrightarrow x=-2\\ 6,\Leftrightarrow x^2-3x+5x-15=0\\ \Leftrightarrow\left(x-3\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
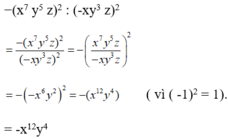
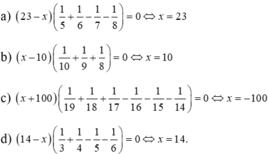
Nếu \(x=25\)
\(\Rightarrow\left\{{}\begin{matrix}26=x+1\\27=x+2\\47=2x-3\\77=3x+2;50=2x;24=x-1\end{matrix}\right.\) ( * )
Thay ( * ) vào C , ta được :
\(C=x^7-\left(x+1\right)x^6+\left(x+2\right)x^5-\left(2x-3\right)x^4-\left(3x+2\right)x^3+2x.x^2+x-\left(x-1\right)\)
\(=x^7-x^7-x^6+x^6+2x^5-2x^5+3x^4-3x^4-2x^3+2x^3+x-x+1\)
\(=1\)
Vậy \(C=1\) tại \(x=25\)