Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(A=2\sqrt{5}-6\sqrt{2}+3\sqrt{5}=5\sqrt{5}-6\sqrt{2}\)
2) \(B=\dfrac{30\left(\sqrt{7}+1\right)}{7-1}+\dfrac{15\left(\sqrt{7}-2\right)}{7-4}=5\sqrt{7}+5+5\sqrt{7}-10=-5+10\sqrt{7}\)
3) \(C=\left(3-\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right)\left(3+\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\right)=\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)=9-5=4\)
4) \(D=3-\sqrt{2}+1-\sqrt{2}=4-2\sqrt{2}\)

a: Ta có: \(\left(4\sqrt{2}-\dfrac{11}{2}\sqrt{8}-\dfrac{1}{3}\sqrt{288}+\sqrt{50}\right)\cdot\left(\dfrac{1}{2}\sqrt{2}\right)\)
\(=\dfrac{1}{2}\sqrt{2}\cdot\left(4\sqrt{2}-11\sqrt{2}-4\sqrt{2}+5\sqrt{2}\right)\)
\(=\dfrac{1}{2}\sqrt{2}\cdot6\sqrt{2}=3\)

Bài 1:
a) Ta có: \(\left(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\sqrt{20}-\dfrac{5}{4}\sqrt{\dfrac{4}{5}}+\sqrt{5}\right)\)
\(=\left(\sqrt{5}+\sqrt{5}-\dfrac{5}{4}\cdot\dfrac{2}{\sqrt{5}}+\sqrt{5}\right)\)
\(=3\sqrt{5}-\dfrac{1}{2}\sqrt{5}\)
\(=\dfrac{5}{2}\sqrt{5}\)
c) Ta có: \(\dfrac{5\sqrt{7}-7\sqrt{5}+2\sqrt{70}}{\sqrt{35}}\)
\(=\dfrac{\sqrt{35}\left(\sqrt{5}-\sqrt{7}+2\sqrt{2}\right)}{\sqrt{35}}\)
\(=2\sqrt{2}+\sqrt{5}-\sqrt{7}\)
Bài 2:
e) ĐKXĐ: \(\dfrac{4}{3}\le x\le6\)
Ta có: \(\sqrt{6-x}=3x-4\)
\(\Leftrightarrow6-x=\left(3x-4\right)^2\)
\(\Leftrightarrow9x^2-24x+16+6-x=0\)
\(\Leftrightarrow9x^2-25x+22=0\)
\(\Delta=\left(-25\right)^2-4\cdot9\cdot22=625-792< 0\)
Vậy: Phương trình vô nghiệm

d: \(=\sqrt{5}\left(\sqrt{3}-1\right)-\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
=căn 5-1/2*căn 5
=1/2*căn 5
e: \(=\dfrac{2\left(\sqrt{8}-\sqrt{3}\right)}{\sqrt{6}\left(\sqrt{3}-\sqrt{8}\right)}-\dfrac{1}{\sqrt{6}}=\dfrac{2}{\sqrt{6}}-\dfrac{1}{\sqrt{6}}=\dfrac{1}{\sqrt{6}}\)
f:=2+căn 3+căn 2-2-căn 3=căn 2

\(2,\\ a,PT\Leftrightarrow\sqrt{\left(5x-1\right)^2}=\sqrt{4\left(x+1\right)^2}\\ \Leftrightarrow\left|5x-1\right|=2\left|x+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}5x-1=2\left(x+1\right)\\1-5x=2\left(x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=3\\7x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{7}\end{matrix}\right.\)
\(b,ĐK:x^2-3\ge0\\ PT\Leftrightarrow\sqrt{x^2-3}=x-1\\ \Leftrightarrow x^2-3=x^2-2x+1\\ \Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ c,ĐK:x\le\dfrac{7}{2}\\ PT\Leftrightarrow7-2x=x^2+7\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\\ d,ĐK:x\ge3\\ PT\Leftrightarrow3\sqrt{x-3}+\dfrac{1}{2}\cdot2\sqrt{x-3}-9\cdot\dfrac{1}{3}\sqrt{x-3}=2\\ \Leftrightarrow\sqrt{x-3}=2\\ \Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)

4: Ta có: \(\dfrac{1}{3+\sqrt{5}}-\dfrac{1}{3-\sqrt{5}}\)
\(=\dfrac{3-\sqrt{5}-3-\sqrt{5}}{4}\)
\(=\dfrac{-\sqrt{5}}{2}\)
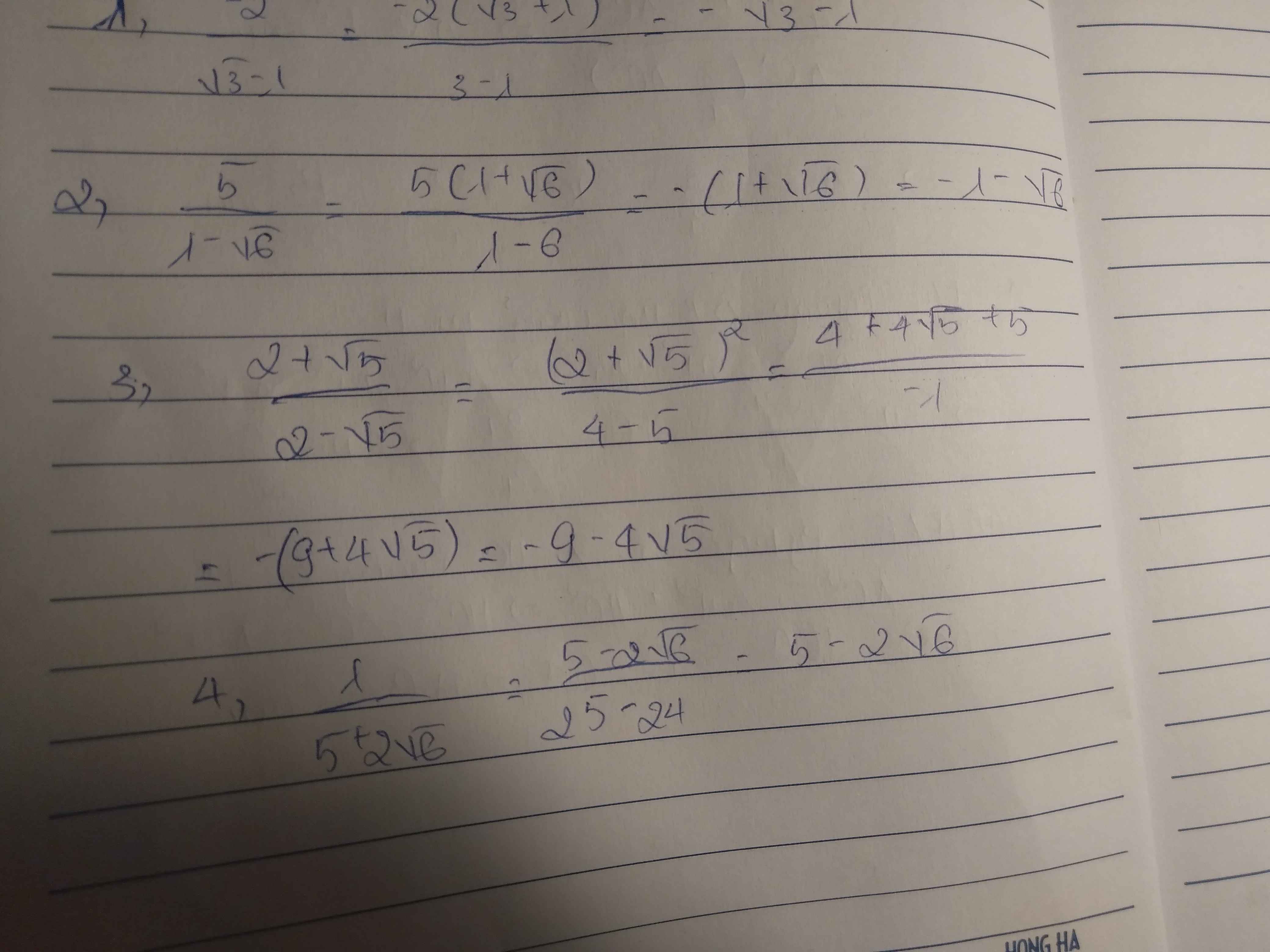
a: \(=\sqrt{\dfrac{1}{10}}+\sqrt{\dfrac{1}{60}}-\dfrac{2\sqrt{15}}{15}\)
\(=\dfrac{\sqrt{10}}{10}-\dfrac{2\sqrt{15}}{15}+\dfrac{\sqrt{15}}{30}\)
\(=\dfrac{3\sqrt{10}-3\sqrt{15}}{30}=\dfrac{\sqrt{10}-\sqrt{15}}{10}\)
b: \(=\dfrac{\left(\sqrt{5}+\dfrac{1}{2}\cdot2\sqrt{5}-\dfrac{5}{4}\cdot\dfrac{2}{\sqrt{5}}+\sqrt{5}\right)}{2\sqrt{5}}\)
\(=\dfrac{\left(\sqrt{5}+\sqrt{5}-\dfrac{1}{2}\sqrt{5}+\sqrt{5}\right)}{2\sqrt{5}}\)
\(=\dfrac{5}{2}:2=\dfrac{5}{4}\)