
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
\(A=\left(1000-1^3\right).\left(1000-2^3\right).........\left(1000-50^3\right)\)
\(A=\left(1000-1^3\right).\left(1000-2^3\right).......\left(1000-10^3\right)........\left(1000-50^3\right)\)
\(A=0.\left(1000-1^3\right).\left(1000-2^3\right)....\left(1000-9^3\right).\left(1000-11^3\right).....\left(1000-50^3\right)\)
A = 0




Bài 7 :43^1 =43. tận cùng là số 3
43^2= 1849 tận cùng là số 9
43^3 =79507 tận cùng là số 7
43^4 =3418801 tận cùng là số 1
43^5 = 147008443 tiếp tục tận cùng là số 3
vậy quy luật của nó cứ lặp đi lặp lại theo dãy 4 số 3 - 9 - 7 - 1
ta có 43 chia 4 dư 3. vậy tận cùng của số 43^43 là 7
tương tự ta có số tận cùng của 17^17 là 7.
vậy thì 43^43 - 17^17 ra số có tận cùng là 0. mà số có tận cùng là 0 thì luôn chia hết cho 10 (điều phải chứng minh)
Bài 8 : \(7^{1000}=\left(7^2\right)^{500}=49^{500}\)
\(3^{1000}=\left(3^2\right)^{500}=9^{500}\)
Ta có : lũy thừa tận cùng là 9 khi nâng bậc lũy thừa chẵn nên tận cùng là 1.
=> \(49^{500}\) tận cùng là 1
=> \(9^{500}\) tận cùng là 1
=> (...1) - (....1) = (....0)
Vì tận cùng là 0 nên chia hết cho 10
Vậy 71000 - 31000 chia hết cho 10 (đpcm)

Dãy số có 2 chữ số chia hết cho 3 là:[12,15,....,99]
Khoảng cách của từng số hạng là 3
Số số hạng là: (99-12):3+1=30(số)
Vậy có 30 số có 2 chữ số chia hết cho 3
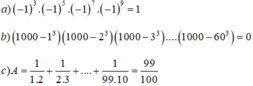
(1000 - 13)(1000 - 23)(1000 - 33)........(1000 - 503)
= (1000 - 13)(1000 - 23)(1000 - 33)....(1000 - 103)....(1000 - 503)
= (1000 - 13)(1000 - 23)(1000 - 33).....(1000 - 1000)...(1000 - 503)
= (1000 - 13)(1000 - 23)(1000 - 33).....0...(1000 - 503)
= 0