Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x}{y+z-3}=\dfrac{y}{x+z}=\dfrac{z}{x+y+3}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=\dfrac{1}{4044\left(x+y+z\right)}\)
\(\Rightarrow\left\{{}\begin{matrix}y+z-3=2x\\x+z=2y\\x+y+3=2z\end{matrix}\right.\) và \(4044\left(x+y+z\right)=2\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=3x+3\\x+y+z=3y\\x+y+z=3z-3\end{matrix}\right.\\ \Rightarrow3x+3=3y=3z-3\\ \Rightarrow x+1=y=z-1\)
\(\left\{{}\begin{matrix}x=y-1\\z=y+1\end{matrix}\right.\)
Lại có \(4044\left(x+y+z\right)=2\)
\(\Rightarrow4044\left(y-1+y+y+1\right)=2\\ \Rightarrow4044\cdot3y=2\\ \Rightarrow y=\dfrac{1}{674}\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{673}{674}\\z=\dfrac{675}{674}\end{matrix}\right.\)

Gợi ý nhá
Bài 3: câu 1: làm tương tự như câu hỏi lần trước bạn gửi.
b) Bạn chỉ cần cho tử và mẫu mũ 3 lên. theé là dễ r
\(\frac{x^3}{8}=\frac{y^3}{64}=\frac{z^3}{216}\Rightarrow=\frac{x}{2}=\frac{y}{4}=\frac{z}{6}\Rightarrow=\frac{x^2}{4}=\frac{y^2}{16}=\frac{z^2}{36}\)
áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{4}=\frac{y^2}{16}=\frac{z^2}{36}=\frac{x^2+y^2+z^2}{4+16+36}=\frac{14}{56}=\frac{1}{4}\)
tự tính tiếp =)

a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
b)
Do đó ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{a}{3}=\frac{b}{2};\frac{b}{7}=\frac{c}{5}\)
Vì \(\frac{a}{3}=\frac{b}{2};\frac{b}{7}=\frac{c}{5}\)
=> \(\frac{a}{3}=\frac{b}{2}\Rightarrow\frac{a}{21}=\frac{b}{14}\)(1)
\(\frac{b}{7}=\frac{c}{5}\Rightarrow\frac{b}{14}=\frac{c}{10}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\Rightarrow\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}\)
Theo tính chất dãy tỉ số bằng nhau:
\(\Rightarrow\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}\Rightarrow\frac{3a-7b+5c}{63-98+50}=\frac{30}{15}=2\)
Do đó: \(\Rightarrow\hept{\begin{cases}\frac{a}{21}=2\Rightarrow a=42\\\frac{b}{14}=2\Rightarrow b=28\\\frac{c}{10}=2\Rightarrow c=20\end{cases}}\)
Vậy: a = 42
b = 28
c = 20
Bài 1:
a)
Ta có: \(\frac{a}{3}=\frac{b}{2}\)
\(\Rightarrow\frac{a}{3}.\frac{1}{7}=\frac{b}{2}.\frac{1}{7}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}\)
Và: \(\frac{b}{7}=\frac{c}{5}\)
=> \(\frac{b}{7}.\frac{1}{2}=\frac{c}{5}.\frac{1}{2}\)
=> \(\frac{b}{14}=\frac{c}{10}\)
Do đó: \(\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau; ta có:
\(\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)\(=\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}=\frac{3a-7b-5c}{63-98-50}\)\(=\frac{30}{-85}\)\(=-\frac{6}{17}\)
+) Với \(\frac{a}{21}=-\frac{6}{17}\Rightarrow a=-\frac{126}{17}\)
+) Với \(\frac{b}{14}=-\frac{6}{17}\Rightarrow b=-\frac{84}{17}\)
+)Với \(\frac{c}{10}=-\frac{6}{17}\Rightarrow c=-\frac{60}{17}\)
Vậỵ:..........
b)
Ta có: 7a = 9b = 21c
=> 7a/63 = 9b/63 = 21c/63
=> a/9 = b/7 = c/3
Áp dụng tính chất dãy tỉ số bằng nhau; ta có:
a/9 = b/7 = c/3 = (a-b+c) / (9-7+3) = -15/5 = -3
+) a/9 = -3 => a = -27
+) b/7 = -3 => b = -21
+) c/3 = -3 => c = -9
Vậy:..............
Bài 2:
a) Theo bài: x:y:z = 5:3:4
=> x/5 = y/3 = z/4
Áp dụng tính chất dãy tiwr số bằng nhau; ta có:
x/5 = y/3 = z/4 = ( x + 2y -z ) / ( 5 + 2.5 - 4 ) = -121 / 11 = -11
+) Với x/5 = -11 => x=-55
+) Với y/3 = -11 => y = -33
+) Với z/4 = -11 => z = -44
Vậy:......
b) _ Tương tự câu a) ở bài 1
c)
Ta đặt: x/3 = y/12 = z/5 = k ( \(k\inℤ\))
=> \(\hept{\begin{cases}x=3k\\y=12k\\z=5k\end{cases}}\)
Theo bài: xyz = 22,5
=> 3k.12k.5k = 22,5
=> 180.k3 = 22,5
=> k3 = 1/8 = (1/2)3
=> k = 1/2
Với k = 1/2 => x = 3/2; y = 6; z = 5/2
Vậy:..........
d)

Cho mik gửi nhờ trang của bn nhé!
Các bn mà làm đúng bài toán mik đưa ra mik cho 20 k.
Bài 1: Không tính kết quả cụ thể, hãy so sánh:
A = abc + mn + 352
B = 3bc + 5n + am2
a) A = a x (b + 1)
B = b x (a + 1) (với a > b)
b) A = 28 x 5 x 30
B = 29 x 5 x 29
Bài 2: Không tính giá trị của biểu thức hãy điền dấu (>; <; =) thích hợp vào chỗ trống:
a) (156 + 78) x 6 .............156 x 6 + 79 x 6
b) (1923 - 172) x 8.............1923 x 8 - 173 x 8
c) (236 - 54) x 7................237 x 7 - 54 x 7
Bài 3: Tính nhanh các giá trị biểu thức dưới đây:
a) 576 + 678 + 780 – 475 - 577 - 679
b) (126 + 32) x (18 - 16 - 2)
c) 36 x 17 x 12 x 34 + 6 x 30
Bài 4: Tìm X:
a) X x 6 = 3048 : 2
b) 56 : X = 1326 – 1318
Bài 5: Với 8 chữ số 8, hãy lập các sao cho tổng các số đó bằng 1000.
Bài 6: Tìm 1 số có 4 chữ số, biết rằng rằng chữ số hàng trăm gấp 3 lần chữ số hàng chục và gấp đôi chữ số hàng nghìn, đồng thời số đó là số lẻ chia hết cho 5.
Bài 7: Tìm số có 2 chữ số, biết rằng nếu viết các chữ số theo thứ tự ngược lại ta sẽ có số mới mà tổng của số phải tìm và số mới bằng 77.
Bài 8: Từ 3 chữ số 2, 3, 8 ta lập được 1 số có 3 chữ số là A. Từ 2 chữ số 2,8 ta lập được 1 số có 2 chữ số khau nhau là B. Tìm số A và B biết hiệu giữa A và B bằng 750.
Bài 9: Từ 3 chữ số 3, 4, 5 viết tất cả các số có ba chữ số (mỗi chữ số không được lặp lại)
Bài 10: Viết số gồm:
a) 5 chục và 5 đơn vị
6 chục và 0 đơn vị
3 nghìn và 3 đơn vị
b) 5 trăm 5 chục và 5 đơn vị
6 trăm 1 chục và 3 đơn vị
60 nghìn 6 trăm và 6 đơn vị
a trăm b chục c đơn vị (a; b; c là chữ số, a khác 0)
Bài 11: Số 540 thay đổi như thế nào nếu:
a) Xoá bỏ chữ số 0
b) Xoá bỏ chữ số 5
c) Thay chữ số 4 bởi chữ số 8
d) Đổi chữ số 4 và chữ số 0 cho nhau
Bài 12:
a) Trường hợp nào tổng của hai số bằng 1 trong hai số hạng của nó?
b) Hai số nào có tổng bằng số bé nhất khác 0?
c) Hai số khác 0 nào có tổng bé nhất?
Bài 13: Hãy viết thêm vào các dãy số sau đây sao cho mỗi dãy có đủ 10 số hạng.
a) 1, 3, 5, 7,...
b) 1, 3, 9, 27,...
c) 1, 4, 5, 9, 14,...
Bài 14: Cho dãy số 1, 4, 7, 10,... Có tất cả 25 số hạng. Em hãy tính xem số hạng cuối cùng là số nào?
Bài 15: Dãy số sau đây có bao số hạng:
1, 6, 11, 16, 21,........................101.
Bài 16: Có 5 hộp bi trong giống nhau nhưng có 1 hộp bi thứ phẩm và 1 viên bi thứ phẩm nhẹ hơn 1 viên bi chính phẩm là 4g. Hỏi làm thế nào chỉ qua 1 lần cân là có thể biết được hộp bi thứ phẩm. (cho biết trước khối lượng của 1 viên bi chính phẩm)
Bài 17: Có 2 kệ sách, kệ thứ nhất nhiều hơn kệ thứ hai 15 quyển, người ta chuyển 6 quyển từ kệ thứ nhất sang kệ thứ hai. Hỏi kệ thứ nhất còn nhiều hơn kệ thứ hai bao nhiêu quyển sách?
Bài 18: Tuổi Hoa bằng 1/4 tuổi mẹ và bằng 1/7 tuổi ông. Ông hơn mẹ 27 tuổi. Hỏi Hoa bao nhiêu tuổi?
Bài 19: Tuổi của bố Mai, mẹ Mai và tuổi của Mai cộng lại là 70 tuổi. Mẹ và Mai có tất cả 35 tuổi. Bố hơn Mai 30 tuổi. Hỏi tuổi của mỗi người là bao nhiêu?
Bài 20: Một cửa hàng trong hai ngày bán được 120 kg gạo, ngày thứ nhất nếu bán được 5 kg gạo nữa thì sẽ gấp 4 lần ngày thứ hai. Hỏi ngày thứ nhất bán được bao nhiêu kg gạo?
Bài 21: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng và có diện tịch bằng 48cm2. Tính chu vi của hình chữ nhật đó.
Ta có :
\(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) và \(x^3+2y^3-3z^3=-64\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\frac{x^3+2y^3-3z^3}{1^3+2.2^3-3.3^3}=\frac{-64}{-64}=1\)
* \(\frac{x}{1}=1\Rightarrow x=1\)
*\(\frac{y}{2}=1\Rightarrow y=2\)
*\(\frac{z}{3}=1\Rightarrow z=3\)
k vs kp với mik đii ạk !

từ \(\frac{x}{2}\)=\(\frac{y}{3}\)=>\(\frac{x}{8}\)=\(\frac{y}{12}\)
\(\frac{y}{4}\)=\(\frac{z}{5}\)=>\(\frac{y}{12}\)=\(\frac{z}{15}\)
=>\(\frac{x}{8}\)=\(\frac{y}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
\(=>\hept{\begin{cases}x=2.8=16\\y=2.12=24\end{cases}z=2.15=30}\)

Hix trình bày đề thiếu chuyên nghiệp :<<
Chỉnh đề: Tìm x, y, z biết:
a) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\) và \(x^2+y^2-z^2=-12\)
b) \(\dfrac{x}{2}=\dfrac{y}{3};\dfrac{y}{4}=\dfrac{z}{5}\) và \(x+y-z=10\)
Giải:
a) Ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{25}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{25}=\dfrac{x^2+y^2-z^2}{4+9-25}=\dfrac{-12}{-12}=1\)
Vậy \(\left\{{}\begin{matrix}x^2=1.4=4\Rightarrow x=\pm2\\y^2=1.9=9\Rightarrow y=\pm3\\z^2=1.25=25\Rightarrow z=\pm5\end{matrix}\right.\)
b) \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{40}=\dfrac{y}{60}\) (1)
\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{60}=\dfrac{z}{75}\) (2)
Từ (1) và (2) suy ra \(\dfrac{x}{40}=\dfrac{y}{60}=\dfrac{z}{75}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
\(\dfrac{x}{40}=\dfrac{y}{60}=\dfrac{z}{75}=\dfrac{x+y-z}{40+60-75}=\dfrac{10}{25}=\dfrac{2}{5}\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{2}{5}.40=16\\y=\dfrac{2}{5}.60=24\\z=\dfrac{2}{5}.75=30\end{matrix}\right.\)
a) Ta có:
x2=y3=z5⇒x24=y29=z225x2=y3=z5⇒x24=y29=z225
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
x24=y29=z225=x2+y2−z24+9−25=−12−12=1x24=y29=z225=x2+y2−z24+9−25=−12−12=1
Vậy ⎧⎪⎨⎪⎩x2=1.4=4⇒x=±2y2=1.9=9⇒y=±3z2=1.25=25⇒z=±5{x2=1.4=4⇒x=±2y2=1.9=9⇒y=±3z2=1.25=25⇒z=±5
b) x2=y3⇒x40=y60x2=y3⇒x40=y60 (1)
y4=z5⇒y60=z75y4=z5⇒y60=z75 (2)
Từ (1) và (2) suy ra x40=y60=z75x40=y60=z75
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
x40=y60=z75=x+y−z40+60−75=1025=25x40=y60=z75=x+y−z40+60−75=1025=25
Vậy ⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩x=25.40=16y=25.60=24z=25.75=30

\(\dfrac{x}{10}\) = \(\dfrac{y}{5}\) ⇒ \(x\) = \(\dfrac{y}{5}\) \(\times\) 10 = 2y
\(\dfrac{y}{2}\) = \(\dfrac{z}{3}\) = ⇒ \(\dfrac{4y}{8}\) = \(\dfrac{4z}{12}\) ⇒ 4z = \(\dfrac{4y}{8}\) \(\times\) 12 = 6y
Theo bài rat ta có:
\(x+4z\) = 2y + 6y = 320 ⇒ 8y = 320 ⇒ y = 320: 8 =40
\(x\) = 40 \(\times\) 2 = 80
z = \(\dfrac{y}{2}\) \(\times\) 3 = \(\dfrac{40}{2}\) \(\times\) 3 = 60
Vậy \(x\) = 80; y = 40; z = 60

Bài làm
Theo tính chất của dãy tỷ số bằng nhau.
Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x^2+y^2-z^2}{4+9-25}=\left(\frac{-12}{-12}\right)=1\)
Từ \(\frac{x}{2}=1\Rightarrow x=1\times2\Rightarrow x=2\)
\(\frac{y}{3}=1\Rightarrow y=1\times3\Rightarrow y=3\)
\(\frac{z}{5}=1\Rightarrow z=1\times5\Rightarrow z=5\)
Vậy x = 2
y = 3
z = 5
Hok Tốt!!!
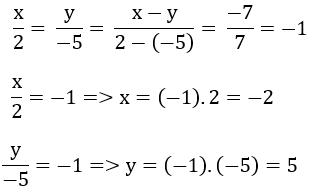
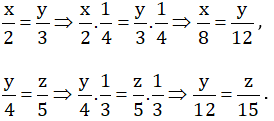
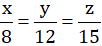
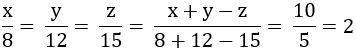
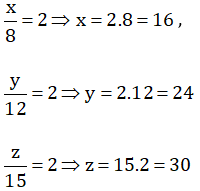
Chúc bạn học tốt!