K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
7 tháng 11 2019
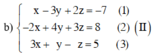
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
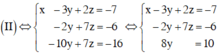
Giải hệ phương trình trên ta được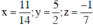 
Vậy hệ phương trình có nghiệm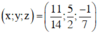 
DM
30 tháng 3 2017
a) \(\left\{{}\begin{matrix}x+3y+2z=8\\2x+2y+z=6\\3x+y+z=6\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\\z=2\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x-3y+2z=-7\\-2x+4y+3z=8\\3x+y-z=5\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{11}{14}\\y=\dfrac{5}{2}\\z=-\dfrac{1}{7}\end{matrix}\right.\)
BT
5 tháng 5 2017
a) Đặt \(\left\{{}\begin{matrix}x+3y+2z=8\left(1\right)\\2x+2y+z=6\left(2\right)\\3x+y+z=6\left(3\right)\end{matrix}\right.\)
Cộng \(\left(2\right)+\left(3\right)\) ta có:\(\left\{{}\begin{matrix}x+3y+2z=8\left(1\right)\\2x+2y+z=6\left(2\right)\\5x+3y+2z=12\left(4\right)\end{matrix}\right.\)
Trừ \(\left(4\right)-\left(1\right)\) ta được: \(4x=4\Leftrightarrow x=1\).
Thay vào hệ phương trình ta được:
\(\left\{{}\begin{matrix}1+3y+2z=8\\2.1+2y+z=6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\z=2\end{matrix}\right.\).
Vậy hệ phương trình có nghiệm: \(\left\{{}\begin{matrix}x=1\\y=1\\z=2\end{matrix}\right.\).
NN
20 tháng 7 2016
a)Vì \(x:y:z=2:3:\left(-4\right)\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{-4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{-4}=\frac{x-y+z}{2-3+-4}=\frac{-125}{-5}=25\)
\(\Rightarrow\begin{cases}\frac{x}{2}=25\\\frac{y}{3}=25\\\frac{z}{-4}=25\end{cases}\)\(\Rightarrow\)\(\begin{cases}x=50\\y=75\\z=-100\end{cases}\)
Vậy x=50;y=75;z=-100
d)Vì 2x=3y\(\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{21}=\frac{y}{14}\)(1)
5y=7z\(\Rightarrow\frac{y}{7}=\frac{z}{5}\Rightarrow\frac{y}{14}=\frac{z}{10}\)(2)
Từ (1) và (2) suy ra:\(\frac{x}{21}=\frac{y}{14}=\frac{z}{10}\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{x}{21}=\frac{y}{14}=\frac{z}{10}=\frac{3x}{63}=\frac{7y}{98}=\frac{5z}{50}=\frac{3x-7y+5z}{63-98+50}=\frac{30}{15}=2\)
\(\Rightarrow\begin{cases}\frac{x}{21}=2\\\frac{y}{14}=2\\\frac{z}{10}=2\end{cases}\)\(\Rightarrow\)\(\begin{cases}x=42\\y=28\\z=20\end{cases}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 12 2020
Lần lượt lấy pt (3) trừ 2 lần pt (1) và pt (2) trừ 3 lần pt (1) ta được:
\(\left\{{}\begin{matrix}y-\left(2m+3\right)z=-3\\y-\left(3m+1\right)z=m-3\end{matrix}\right.\)
Hệ đã cho có vô số nghiệm khi và chỉ khi:
\(\dfrac{1}{1}=\dfrac{3m+1}{2m+3}=\dfrac{m-3}{-3}\) (ko tồn tại m thỏa mãn)
Vậy ko tồn tại m để hệ có vô số nghiệm
E
24 tháng 10 2018
\(5x=8y=20z\Rightarrow\dfrac{x}{160}=\dfrac{y}{100}=\dfrac{z}{40}=\dfrac{x-y-z}{160-100-40}=\dfrac{3}{20}\)
\(\Rightarrow\left\{{}\begin{matrix}x=24\\y=15\\z=6\end{matrix}\right.\)
HH
24 tháng 10 2018
Lần sau đăng ở mục Toán 7 nha bạn :)
\(5x=8y=20z\Leftrightarrow\left\{{}\begin{matrix}5x=8y\\8y=20z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{8}=\dfrac{y}{5}\\\dfrac{y}{20}=\dfrac{z}{8}\end{matrix}\right.\Leftrightarrow\dfrac{x}{32}=\dfrac{y}{20}=\dfrac{z}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{32}=\dfrac{y}{20}=\dfrac{z}{8}=\dfrac{x-y-z}{32-20-8}=\dfrac{3}{4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{4}.32=24\\y=\dfrac{3}{4}.20=15\\z=\dfrac{3}{4}.8=6\end{matrix}\right.\)
Vậy ...
TP
0
AH
Akai Haruma
Giáo viên
7 tháng 7 2017
Lời giải:
Đặt \((x,y,z)=(a+1,b+1,c+1)\Rightarrow a,b,c\geq 0\)
Ta có:
\(3x^2+4y^2+5z^2=52\Leftrightarrow 3(a+1)^2+4(b+1)^2+5(c+1)^2=52\)
\(\Leftrightarrow 3a^2+4b^2+5c^2+6a+8b+10c=40\)
\(\Leftrightarrow 5(a+b+c)^2+10(a+b+c)=40+2a^2+b^2+10(ab+bc+ac)+4a+2b\)
\(\Rightarrow 5(a+b+c)^2+10(a+b+c)\geq 40\Leftrightarrow a+b+c\geq 2\)
Do đó \(x+y+z=a+b+c+3\geq 5\)
Vậy \(F_{\min}=5\Leftrightarrow x=y=1,z=3\)
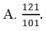
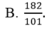
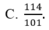
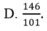
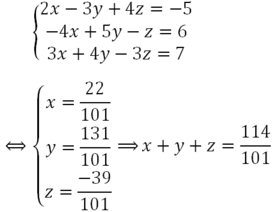
Bài toán :
Kết quả: Giải hệ phương trình