NT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
4 tháng 5 2019
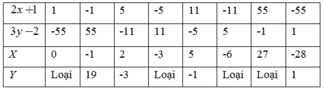
a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
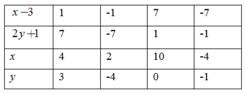
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.
NT
0
TH
0
KK
1
6 tháng 2 2018
a) Do (x-3).(2y+1)=7
nên (x-3),(2y+1) thuộc Ư(7)
mà Ư(7)={1;-1;7;-7}
mà 2y+1 là số nguyên lẻ
nên x-3 thuộc {1;-1;7;-7}
2y+1 thuộc {7;-7;1;-1}
nên x thuộc {4;2;10;-4}
2y thuộc {6;-8;0;-2}= y thuộc {3;-4;0;-1}
NT
0
VP
2
9 tháng 2 2017
a) (x-3).(2y+1)=7 có \(7=1.7=-1.-7\) nên ta có các trường hợp sau:
∙ Nếu \(\left\{\begin{matrix}x-3=1\\3y+1=7\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}x=4\\y=3\end{matrix}\right.\)
∙ Nếu \(\left\{\begin{matrix}x-3=7\\2y+1=1\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}x=10\\y=0\end{matrix}\right.\)
∙ Nếu \(\left\{\begin{matrix}x-3=-1\\2y+1=-7\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}x=2\\y=-4\end{matrix}\right.\)
∙ Nếu \(\left\{\begin{matrix}x-3=-7\\2y+1=-1\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}x=-4\\y=-1\end{matrix}\right.\)
Vậy: \(\left(x;y\right)=\left(4;3\right),\left(10;0\right),\left(2;-4\right),\left(-4;-1\right)\)
9 tháng 2 2017
b) (2x+1).(3y-2)=-55
\(\Rightarrow2x+1=-\frac{55}{3y-2}\left(1\right)\)
Để \(x\in Z\) thì \(3y-2\inƯ_{\left(55\right)}=-55;-11;-5;-1;1;5;11;55\)
* \(3y-2=55\Rightarrow3y=57\Rightarrow y=19\) thay vào \(\left(1\right)\Rightarrow x=0\)
* \(3y-2=11\Rightarrow3y=13\Rightarrow y=\frac{13}{3}\) ( loại )
* \(3y-2=5\Rightarrow3y=7\Rightarrow y=\frac{7}{3}\) ( loại )
* \(3y-2=1\Rightarrow3y=3\Rightarrow y=1\) thay vào \(\left(1\right)\Rightarrow x=-28\)
* \(3y-2=-1\Rightarrow3y=1\Rightarrow y=\frac{1}{3}\) ( loại )
* \(3y-2=-5\Rightarrow3y=-3\Rightarrow y=-1\) thay vào \(\left(1\right)\Rightarrow x=-6\) * \(3y-2=-11\Rightarrow3y=-9\Rightarrow y=-3\) thay vào \(\left(1\right)\Rightarrow x=-28\) * \(3y-2=-55\Rightarrow3y=-53\Rightarrow y=-\frac{53}{3}\) ( loại ) Vậy: Ta có 4 cặp số \(\left(x;y\right)\) thỏa mãn là: \(\left(x;y\right)=\left(0;19\right),\left(-28;1\right),\left(-6;-1\right),\left(-28;-3\right)\)
TT
1
TH
1
10 tháng 4 2022
a: (x-1)(y+1)=5
nên \(\left(x-1;y+1\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
hay \(\left(x,y\right)\in\left\{\left(2;4\right);\left(6;0\right);\left(0;-6\right);\left(-4;-2\right)\right\}\)
b: (x-3)(2y+1)=7
\(\Leftrightarrow\left(x-3;2y+1\right)\in\left\{\left(1;7\right);\left(7;1\right);\left(-1;-7\right);\left(-7;-1\right)\right\}\)
hay \(\left(x,y\right)\in\left\{\left(4;3\right);\left(10;0\right);\left(2;-4\right);\left(-4;-1\right)\right\}\)
a) (x-3).(2y+1)=7
(x-3).(2y+1)= 1.7 = (-1).(-7)
Cứ cho x - 3 = 1 => x= 4
2y + 1 = 7 => y = 3
Tiếp x - 3 = 7 => x = 10
2y + 1 = 1 => y = 0
x-3 = -1 ...
mình giải cho bạn câu a câu b tương tự
(x-3)(2y+1)=7
ta nhân các vế với nhau được
2xy+x-6x-3=7
=2xy-5x=10
=x(2y+5)=10
mà 10 có các số tích với nhau là 2 vs 5 và 10vs 1
rùi thế vào tính x,y