K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NA
5
6 tháng 9 2015
(x-42) - 17 = 127
=> x - 42 = 127 + 17 = 144
=> x = 144 + 42 = 186
23(x+1) = 69
=> x + 1 = 69 : 23 = 3
x = 3 - 1 = 2
2x + 5 = 120 : 2 = 60
=> 2x = 60 - 5 = 55
x = 55 : 2 = 27,5
5x - 2 = 613
=> 5x = 613 + 2 = 615
x = 615 : 5 = 123
6 tháng 9 2015
a)(x-42)-17=127
(x-42)=127+17
(x-42)=144
x=144+42
x=186
b)23(x+1)=69
(x+1)=69:23
(x+1)=3
x=3-1
x=2
c)2.x+5=120:2
2.x+5=60
2.x=60-5
2.x=55
x=55:2
x=27,5
d)5.x-2=613
5.x=613+2
5.x=615
x=615:5
x=123
18 tháng 8 2021
Bài 1:
Ta có: \(4-2\left(x+1\right)=2\)
\(\Leftrightarrow2\left(x+1\right)=2\)
\(\Leftrightarrow x+1=1\)
hay x=0
Bài 2:
Ta có: \(\left|2x-3\right|-1=2\)
\(\Leftrightarrow\left|2x-3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
2 tháng 2 2023
Lời giải:
a. Để $B$ là phân số thì $x+3\neq 0\Leftrightarrow x\neq -3$
b. Để $B$ nhận giá trị nguyên thì $x+3$ là ước của $7$
$\Rightarrow x+3\in\left\{1;-1;7;-7\right\}$
$\Rightarrow x\in\left\{-2; -4; 4; -10\right\}$
c. Để $B< 0$ thì $7$ và $x+3$ trái dấu nhau. Mà $7>0$ nên $x+3<0$
$\Leftrightarrow x<-3$
d. Để $B$ đạt giá trị lớn nhất thì $x+3$ là số dương nhỏ nhất.
Với $x$ nguyên, $x+3$ dương nhỏ nhất bằng $1$
Khi đó: $B_{\max}=\frac{7}{1}=7$. Giá trị này đạt tại $x+3=1$ hay $x=-2$
b) 
d) 
Bài 2: Tìm x biết:
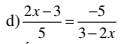
\(\dfrac{2x-3}{5}=\dfrac{-5}{3-2x}\) ĐK `3-2x≠0<=>x≠3/2`
\(\Leftrightarrow\dfrac{\left(2x-3\right)\left(3-2x\right)}{5\left(3-2x\right)}=\dfrac{-5.5}{5\left(3-2x\right)}\)
`=> (2x-3)(3-2x)=-25`
`<=>6x-4x^2-9+6x=-25`
`<=> -4x^2 +12x=-25+9`
`<=> -4x^2 +12x+16=0`
`<=> -4(x-4)(x+1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-1\end{matrix}\right.\)
vậy phương trình có tập nghiệm \(S=\left\{4;-1\right\}\)
ĐK là gì thế bn