PD
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 3 2016
\(\Leftrightarrow\frac{1}{2}+\left(\frac{2}{56}+\frac{2}{72}+...+\frac{2}{x\left(x+1\right)}\right)=\frac{3}{10}\)
\(\Leftrightarrow\frac{1}{2}+2.\left(\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}+...+\frac{1}{x}-\frac{1}{x+1}\right)=\frac{3}{10}\)
\(\Leftrightarrow2.\left(\frac{1}{7}-\frac{1}{x+1}\right)=\frac{3}{10}-\frac{1}{2}=-\frac{1}{5}\)
\(\Leftrightarrow\frac{1}{7}-\frac{1}{x+1}=-\frac{1}{5}:2=-\frac{1}{10}\)
\(\Leftrightarrow\frac{1}{x+1}=\frac{1}{7}-\left(-\frac{1}{10}\right)=\frac{17}{70}\)
\(\Rightarrow17x+17=70\)
=> không tồn tại n vì n là số tự nhiên
SY
12 tháng 3 2016
bạn ơi, mình biết làm bài này nhưng cho mình biết làm sao để viết phân số vậy
1 tháng 2 2016
x-1 là ước của 2^2-2x+3
=>7-2x chia hết cho x-1
=>2-2x+5 chia hết cho x-1
=>-2.(x-1)+5 chia hết cho x-1
=>5 chia hết cho x-1
=>x-1 thuộc U(5)={1;-1;5;-5}
=>x={2;0;6;-4}
1 tháng 2 2016
x-1 là ước của 2^2-2x+3
=>7-2x chia hết cho x-1
=>2-2x+5 chia hết cho x-1
=>-2.(x-1)+5 chia hết cho x-1
=>5 chia hết cho x-1
=>x-1 thuộc U(5)={1;-1;5;-5}
=>x={2;0;6;-4}
1 tháng 2 2016
x-1 là ước của 2^2-2x+3
=>7-2x chia hết cho x-1
=>2-2x+5 chia hết cho x-1
=>-2.(x-1)+5 chia hết cho x-1
=>5 chia hết cho x-1
=>x-1 thuộc U(5)={1;-1;5;-5}
=>x={2;0;6;-4}
1 tháng 2 2016
x-1 là ước của 2^2-2x+3
=>7-2x chia hết cho x-1
=>2-2x+5 chia hết cho x-1
=>-2.(x-1)+5 chia hết cho x-1
=>5 chia hết cho x-1
=>x-1 thuộc U(5)={1;-1;5;-5}
=>x={2;0;6;-4}
1 tháng 2 2016
x-1 là ước của 2^2-2x+3
=>7-2x chia hết cho x-1
=>2-2x+5 chia hết cho x-1
=>-2.(x-1)+5 chia hết cho x-1
=>5 chia hết cho x-1
=>x-1 thuộc U(5)={1;-1;5;-5}
=>x={2;0;6;-4}
23 tháng 2 2017
a,\(\dfrac{3x+5}{x-2}=3+\dfrac{11}{x-2}\)
\((3x+5)\vdots (x-2)\) \(\Rightarrow\)\(\dfrac{3x+5}{x-2}\)nguyên \(\Rightarrow \dfrac{11}{x-2}\)nguyên
\(\Rightarrow 11\vdots(x-2)\Rightarrow (x-2)\in Ư(11)=\{\pm1;\pm11\}\)
\(\Rightarrow x\in\{-9;1;3;13\}\)
b,\(\dfrac{2-4x}{x-1}=-4-\dfrac{2}{x-1}\)
\((2-4x)\vdots(x-1)\Rightarrow \dfrac{2-4x}{x-1}\)nguyên\(\Rightarrow \dfrac{2}{x-1}\)nguyên
\(\Rightarrow 2\vdots(x-1)\Rightarrow (x-1)\inƯ(2)=\{\pm1;\pm2\}\\\Rightarrow x\in\{-1;0;2;3\}\)
c,\(\dfrac{x^{2}-x+2}{x-1}=\dfrac{x(x-1)+2}{x-1}=x+\dfrac{2}{x-1}\)
\((x^{2}-x+2)\vdots(x-1)\)\(\Rightarrow \dfrac{x^{2}-x+2}{x-1}\)nguyên \(x+\dfrac{2}{x-1}\)nguyên\(\Rightarrow \dfrac{2}{x-1}\)nguyên
\(\Rightarrow 2\vdots(x-1)\Rightarrow (x-1)\inƯ(2)=\{\pm1;\pm2\}\\\Rightarrow x\in\{-1;0;2;3\}\)
d,\(\dfrac{x^{2}+2x+4}{x+1}=\dfrac{(x+1)^{2}+3}{x+1}=x+1+\dfrac{3}{x+1}\)
\((x^{2}+2x+4)\vdots(x+1)\Rightarrow \dfrac{x^{2}+2x+4}{x+1}\in Z\Rightarrow \dfrac{3}{x+1}\in Z\\\Rightarrow3\vdots(x+1)\Rightarrow (x+1)\in Ư(3)=\{\pm1;\pm3\}\\\Rightarrow x\in\{-4;-2;0;2\}\)
CM
27 tháng 2 2019
Đáp án C.
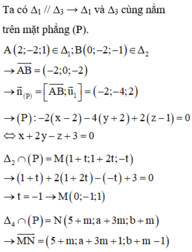
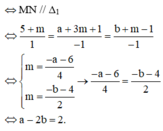
Không tồn tại đường thẳng nào trong không gian cắt cả 4 đường thẳng đã cho
Ta có : \(\frac{1}{21}+\frac{1}{28}+...+\frac{2}{x\left(x+1\right)}=\frac{2}{9}\)
\(\Rightarrow\frac{2}{42}+\frac{2}{56}+...+\frac{2}{x\left(x+1\right)}=\frac{2}{9}\)
\(\Rightarrow2\left(\frac{1}{42}+\frac{1}{56}+...+\frac{1}{x\left(x+1\right)}\right)=\frac{2}{9}\)
\(\Rightarrow2\left(\frac{1}{6.7}+\frac{1}{7.8}+...+\frac{1}{x\left(x+1\right)}\right)=\frac{2}{9}\)
\(\Rightarrow2\left(\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+...+\frac{1}{x}-\frac{1}{x+1}\right)=\frac{2}{9}\)
\(\Rightarrow2\left(\frac{1}{6}-\frac{1}{x+1}\right)=\frac{2}{9}\)
\(\Rightarrow\frac{1}{6}-\frac{1}{x+1}=\frac{2}{9}:2=\frac{1}{9}\)
\(\Rightarrow\frac{1}{x+1}=\frac{1}{6}-\frac{1}{9}=\frac{1}{18}\)
\(\Rightarrow x+1=18\Rightarrow x=17\)
Vậy x = 17
\(\Rightarrow\dfrac{2}{42}+\dfrac{2}{56}+\dfrac{2}{72}+.....+\dfrac{2}{x\left(x+1\right)}\Rightarrow2\left(\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+.....+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{2}{9}\\ \Rightarrow2\left(\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+....+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{2}{9}\\ \Rightarrow2\left(\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+....+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{2}{9}\\ \Rightarrow2\left(\dfrac{1}{6}-\dfrac{1}{x+1}\right)=\dfrac{2}{9}\\ \Rightarrow\dfrac{1}{6}-\dfrac{1}{x+1}=\dfrac{2}{9}:2\\ \Rightarrow\dfrac{1}{6}-\dfrac{1}{x+1}=\dfrac{2}{9}.\dfrac{1}{2}\\ \Rightarrow\dfrac{1}{6}-\dfrac{1}{x+1}=\dfrac{1}{9}\\ \Rightarrow\dfrac{1}{x+1}=\dfrac{1}{6}-\dfrac{1}{9}\\ \Rightarrow\dfrac{1}{x+1}=\dfrac{3}{54}\\ \Rightarrow x+1=\dfrac{54}{3}\\ \Rightarrow x=\dfrac{54}{3}-1=\dfrac{51}{3}\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \)