Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)

a)\(f\left(x\right)=2x^2-x-3+5=\left(x+1\right)\left(2x-3\right)+5\)
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(x+1\right)\left(2x-3\right)+5⋮\left(x+1\right)\)
\(\Leftrightarrow5⋮\left(x+1\right)\)
mà \(x+1\in Z\Rightarrow x+1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{-2;0;4;-6\right\}\)
Vậy...
b) \(f\left(x\right)=3x^2-4x+6=\left(3x^2-4x+1\right)+5=\left(3x-1\right)\left(x-1\right)+5\)
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(3x-1\right)\left(x-1\right)+5⋮\left(3x-1\right)\)
\(\Leftrightarrow5⋮\left(3x-1\right)\) mà \(3x-1\in Z\Rightarrow3x-1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{0;\dfrac{2}{3};2;-\dfrac{4}{3}\right\}\) mà x nguyên\(\Rightarrow x\in\left\{0;2\right\}\)
Vậy...
c)\(f\left(x\right)=\left(-2x^3-7x^2-5x+2\right)+3\)\(=\left(-2x^3-4x^2-3x^2-6x+x+2\right)+3\)\(=\left[-2x^2\left(x+2\right)-3x\left(x+2\right)+\left(x+2\right)\right]+3\)
\(=\left(x+2\right)\left(-2x^2-3x+1\right)+3\)
Làm tương tự như trên \(\Rightarrow x+2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Leftrightarrow x\in\left\{-5;-3;-1;1\right\}\)
Vậy...
d)\(f\left(x\right)=x^3-3x^2-4x+3=x\left(x^2-3x-4\right)+3=x\left(x+1\right)\left(x-4\right)+3\)
Làm tương tự như trên \(\Rightarrow x+1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow x\in\left\{-4;-2;0;2\right\}\)
Vậy...

Lời giải:
a. $f(x)=x^4-3x^2+2x-7=x^3(x+2)-2x^2(x+2)+x(x+2)-7$
$=(x+2)(x^3-2x^2+x)-7=g(x)(x^3-2x^2+x)-7$
Vậy $f(x)$ chia $g(x)$ được thương là $x^3-2x^2+x$ và dư là $-7$
b. Theo phần a $f(x)=(x^3-2x^2+x)g(x)-7$
Với $x$ nguyên, để $f(x)\vdots g(x)$ thì $7\vdots g(x)$
$\Leftrightarrow x+2$ là ước của $7$
$\Rightarrow x+2\in\left\{\pm 1;\pm 7\right\}$
$\Leftrightarrow x\in\left\{-3; -1; 5; -9\right\}$
c.
Theo định lý Bezout về phép chia đa thức, để $K(x)=-2x^3+x-m\vdots x+2$ thì: $K(-2)=0$
$\Leftrightarrow -2(-2)^3+(-2)-m=0$
$\Leftrightarrow 14-m=0$
$\Leftrightarrow m=14$

Ta có
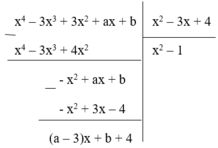
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !

Để f(x) chia hết cho g(x). Áp dụng định lý Bozu ta được:
f(3/2) =0 <=> f(3/2)= 2 *(3/2)^3 -7*(3/2)^2 +5*3/2 +m=0
<=>-3/2 +m=0 <=> m=3/2
f(x) = 2x^3 - 7x^2 + 5x + m
= 2x^3 - 3x^2 - 4x^2 + 6x - x + m
= x^2 (2x - 3) - 2x( 2x - 3) - (x - m)
= (2x - 3) (x^2 - 2x) - (x-m) chia chết cho g(x) = 2x - 3
--> x - m chia hết cho 2x - 3
-> 2x - 2m cũng chia hết cho 2x - 3
Gọi 2x - 2m = (2x - 3) * k
Ta có : 2x - 2m = 2xk - 3k
Áp dụng phương pháp đồng nhất thức hệ số, suy ra k = 1 và 3k = 2m
Suy ra, m = 3/2 * k = 3/2 * 1 = 3/2.
Vậy m = 3/2